Cách tính đường chéo hình vuông, cách tính đường chéo hình chữ nhật được sử dụng rất nhiều trong các bài toán và ứng dụng thực tế như thiết kế và xây dựng, cắt góc, đo lường... Quantrimang.com đã tổng hợp những kiến thức về tính chất của hai đường chéo cũng như công thức tính, mời các bạn tham khảo để áp dụng trong học tập, cuộc sống và công việc.
Đéo chéo hình vuông, hình chữ nhật là gì
Đường chéo của hình vuông, hình chữ nhật là đường thẳng nối hai góc đối diện. Mỗi hình vuông, hình chữ nhật có hai đường chéo với độ dài bằng nhau.
Cách tính đường chéo hình vuông
Tính chất đường chéo hình vuông
- 2 đường chéo của hình vuông có chiều dài bằng nhau, vuông góc và giao nhau tại trung điểm của mỗi đường.
- Có một đường tròn nội tiếp và ngoại tiếp đồng thời tâm của cả hai đường tròn trùng nhau và là giao điểm của hai đường chéo của hình vuông.
- 1 đường chéo sẽ chia hình vuông thành hai tam giác vuông cân.
- Giao của các đường phân giác, trung tuyến, trung trực đều trùng tại một điểm.
- Có tất cả tính chất của hình chữ nhật, hình bình hành và hình thoi.
Công thức tính đường chéo của hình vuông
Theo tính chất hình vuông thì hai đường chéo hình vuông bằng nhau và 1 đường chéo hình vuông sẽ chia hình vuông thành hai phần có diện tích bằng nhau chính là 2 tam giác vuông cân, như vậy đường chéo hình vuông chính là cạnh huyền của 2 tam giác vuông cân đó.
Vậy để tính đường chéo hình vuông các bạn chỉ cần áp dụng định lý Pytago cho tam giác vuông.
Giả sử các bạn có hình vuông ABCD độ dài cạnh a, đường chéo AC chia hình vuông thành 2 tam giác vuông cân ABC và ACD.
Ví dụ về tính đường chéo hình vuông
Ví dụ 1: Một hình vuông có cạnh bằng 3cm. Đường chéo của hình vuông đó bằng: 6cm, √18cm, 5cm, hay 4cm?
Bài giải:
a) Áp dụng định lí Pi-ta-go trong hình vuông ABC, ta có:
AC² = AB² + BC² = 3² + 3² = 18
=> AC =  cm
cm
Vậy đường chéo của hình vuông bằng √18 cm .
Ví dụ 2:
Đường chéo của một hình vuông bằng 2dm. Cạnh của hình vuông đó bằng: 1cm, 3/2cm, √2cm hay 4/3cm?
Giải:
Áp dụng định lí Py-ta-go vào tam giác vuông ABC, nhưng bài này cho độ dài đường chéo, tức AC = 2cm, tính cạnh AB.
Ta có: AC² = AB² + BC² = 2AB (vì AB = BC)
=> AB² = AC²/2 = 2²/2 = 2
=> AB = √2
Cách tính đường chéo hình chữ nhật
Hình chữ nhật là một hình tứ giác lồi có bốn góc vuông, đây là hình bình hành có hai đường chéo bằng nhau.
Tính chất đường chéo hình chữ nhật
Đường chéo của hình chữ nhật có một số tính chất quan trọng, rất hữu ích trong việc giải quyết các bài toán liên quan đến hình chữ nhật và đường chéo của nó.
- Độ dài đường chéo của hình chữ nhật là cạnh huyền của một tam giác vuông nên bằng căn bậc hai của tổng bình phương hai cạnh.
- Đường chéo chia hình chữ nhật thành hai tam giác vuông có diện tích bằng nhau. Vì vậy, đường chéo của hình chữ nhật là trục đối xứng của hình chữ nhật.
- Hai đường chéo của hình chữ nhật bằng nhau và cắt nhau tại trung điểm của mỗi đường và tạo thành 4 tam giác cân.
Công thức tính đường chéo hình chữ nhật
Từ các tính chất của đường chéo hình chữ nhật ở trên, ta có thể sử dụng định lý Pytago để tính độ dài đường chéo hình chữ nhật.
Giả sử các bạn có hình chữ nhật ABCD có độ dài chiều dài là a và độ dài chiều rộng là b, đường chéo AC như hình vẽ dưới.
Như vậy, chỉ cần áp dụng định lý Pytago là chúng ta có thể tính được đường chéo hình vuông hay hình chữ nhật.
Ví dụ về tính đường chéo hình chữ nhật
Tính độ dài đường chéo hình chữ nhật biết chiều dài bằng 10dm và chiều rộng bằng 5dm.
Lời giải:
Gọi độ dài đường chéo hình chữ nhật là a (a > 0, dm)
Áp dụng định lý Pitago, độ dài đường chéo của hình chữ nhật là:
a2 = 102 + 52 = 125
=> a = 5√5 dm
Ví dụ chứng minh tứ giác là hình chữ nhật.
Có thể áp dụng tính chất, công thức tính đường chéo hình chữ nhật để áp dụng giải một số bài toán chứng minh tứ giác là hình chữ nhật.
Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, AD. Tứ giác EFGH là hình gì? Vì sao?
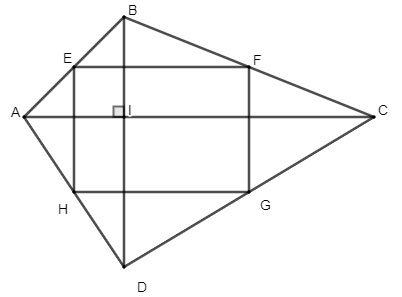
Lời giải:
Vì E là trung điểm của AB, H là trung điểm của AD
=> EH là đường trung bình của tam giác ABD.
(1)
Vì F là trung điểm của BC, G là trung điểm của CD
=> FG là đường trung bình của tam giác BCD
(2)
Từ (1) và (2) =>
Xét tứ giác EFGH có
FG // EH
FG = EH
=> EFGH là hình bình hành (dấu hiệu nhận biết)
Mặt khác:
Lại có :
E là trung điểm của AB, F là trung điểm của BC.
=> EF là đường trung bình của tam giác ABC
=> EF // AC
Mà EH ⊥ AC => EH ⊥ EF
Hình bình hành EFGH có một góc vuông
=> EFGH là hình chữ nhật