
1968 mệnh gì? Hợp tuổi nào, hướng nào? Xem phong thủy 1968
1968 mệnh gì? Sinh năm 1968 thuộc tuổi con gì? Cùng YODY tìm hiểu từ A - Z với bài viết chi tiết dưới đây nhé!
1. 1968 mệnh gì?
Sinh năm 1968 mệnh gì? Chắc chắn, bạn mang mệnh Thổ. Mệnh Thổ đại diện cho đất, tượng trưng cho sự bình an và may mắn. Những người mang mệnh Thổ thường có tính cách ôn hòa, hiền hậu, yêu thương, cần cù và chăm chỉ.
Việc tìm hiểu về mệnh cũng như các hướng và màu tương sinh, tương khắc trong phong thủy thường là thói quen phổ biến của nhiều gia chủ khi xây nhà hoặc mua xe, để tạo ra một môi trường sống và phương tiện đi lại hợp phong thủy, đem lại nhiều may mắn và tài lộc cho bản thân và gia đình.
Nếu bạn sinh năm 1968, bạn nên tìm hiểu thêm về các yếu tố phong thủy như hướng nhà và màu xe phù hợp với mệnh Thổ của mình. Điều này có thể giúp bạn tránh những vận xui và tai họa không mong muốn.

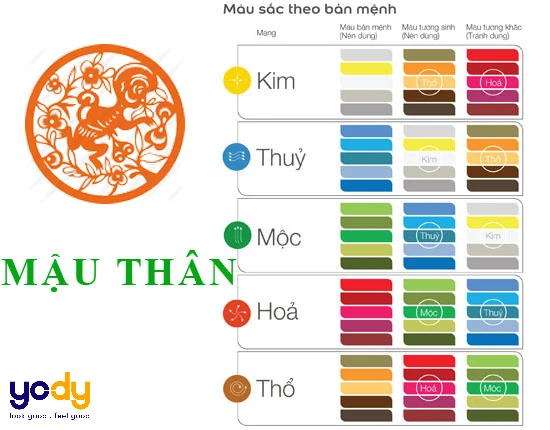
1968 mệnh gì, hợp màu gì?
Mệnh Thổ tương sinh với mệnh Kim và mệnh Hỏa, trong khi tương khắc với mệnh Thủy và mệnh Mộc. Việc hiểu rõ về các tương tác này có thể giúp bạn tối ưu hóa môi trường sống và đạt được cân bằng và hài hòa trong cuộc sống.
2. Sinh năm 1968 tuổi con gì?
Người sinh năm 1968, tuổi Thân (Mậu Thân) - hay còn được gọi là tuổi Khỉ - được biết đến với sự thông minh và sự hoạt bát của mình. Khỉ là một loài động vật rất thông minh, lanh lẹ và nhanh nhẹn, và những người sinh trong năm Khỉ thường có những đặc điểm tương tự.
Bất kể nam hay nữ, người sinh năm 1968 đều có tinh thần tiếp thu và khao khát học hỏi những điều mới. Họ sở hữu sự nhạy bén trong việc giải quyết các vấn đề và rất tài giỏi.
Đối với phụ nữ sinh năm Thân, họ có tính cách kiên định, luôn giữ vững lập trường và không bị ảnh hưởng dễ dàng bởi những yếu tố bên ngoài. Tuy nhiên, dù có tâm hồn tốt, họ không phải lúc nào cũng giỏi trong việc thể hiện tình cảm của mình. Điều này dẫn đến sự hiểu lầm và khó khăn trong mối quan hệ với người khác.

1968 tuổi con gì?
Nam sinh năm Thân thường rất thông minh, vui tươi và hài hước. Họ có tính tò mò cao đối với mọi thứ xung quanh. Đôi khi, họ thích đùa giỡn để tạo không khí vui vẻ, nhưng cũng cần lưu ý để không làm tổn thương người khác. Đặc biệt, nam tuổi Thân thường cứng đầu, không muốn trưởng thành và không dễ chấp nhận ý kiến của người khác. Họ luôn kiên quyết giữ vững quan điểm riêng và ít khi tin tưởng và nghe theo ý kiến của người khác.
Tóm lại, người sinh năm 1968, tuổi Thân (Mậu Thân) - tuổi Khỉ, có những đặc điểm như thông minh, nhanh nhẹn, tài giỏi và hoạt bát. Tuy nhiên, nữ tuổi Thân có thể gặp khó khăn trong việc thể hiện tình cảm và nam tuổi Thân thường cứng đầu và không dễ chấp nhận ý kiến của người khác.
3. Tuổi Mậu Thân 1968 hợp màu gì?
Người sinh năm 1968 có mệnh Thổ và nên lựa chọn những gam màu phù hợp với mệnh Thổ để thu hút may mắn và tài lộc. Dưới đây là những màu sắc hợp với mệnh Thổ:
- Màu đỏ: Đỏ là màu thuộc hành Hỏa, tượng trưng cho sự nhiệt huyết, may mắn và tài lộc. Gia chủ tuổi Mậu Thân có thể chọn các gam đỏ như đỏ rực, đỏ cam để mang lại sự may mắn và sức sống.
- Màu cam: Cam cũng là một gam màu thuộc hành Hỏa, biểu trưng cho sự sáng tạo, nhiệt huyết và phát triển. Sử dụng các màu cam như cam đất, cam rực sẽ giúp gia chủ tuổi Mậu Thân thu hút sự thành công và tài lộc.

Màu đỏ là màu sắc phủ hợp với 1968
- Màu hồng: Hồng là một gam màu nhẹ nhàng và tinh tế, biểu thị sự tình yêu, hạnh phúc và may mắn. Sử dụng màu hồng trong trang phục, phụ kiện hoặc trang trí nhà cửa sẽ mang đến cảm giác yêu thương và sự may mắn cho gia đình.
- Màu tím: Tím cũng thuộc hành Hỏa và biểu trưng cho sự quý phái, sự giàu có và tinh thần cao quý. Sử dụng các gam màu tím như tím than, tím lục, tím cánh sen sẽ mang lại cảm giác sang trọng và may mắn cho gia chủ tuổi Mậu Thân.
4. Sinh năm 1968 cung mệnh gì?
Người sinh năm 1968 có cung mệnh khác nhau tùy thuộc vào giới tính. Gia chủ nam sinh năm 1968 thuộc cung mệnh Khôn, trong khi gia chủ nữ sinh năm 1968 thuộc cung mệnh Khảm.
- Cung mệnh Khôn (Nam): Gia chủ nam sinh năm 1968 thuộc cung mệnh Khôn. Cung mệnh này biểu thị sự thông minh, sắc bén và khả năng lãnh đạo. Những người thuộc cung mệnh Khôn thường có tinh thần phiêu lưu, đam mê khám phá, và có năng lực tự tin trong việc giải quyết các vấn đề phức tạp.
- Cung mệnh Khảm (Nữ): Gia chủ nữ sinh năm 1968 thuộc cung mệnh Khảm. Cung mệnh này biểu thị sự yếu đuối, nhạy cảm và tình cảm. Những người thuộc cung mệnh Khảm thường có trực giác sắc bén, khả năng cảm nhận tốt về người khác và có khả năng thấu hiểu và chăm sóc người khác.
Nữ sinh năm 1968 mệnh gì? Nam sinh năm 1968 mệnh gì?
Tuy cung mệnh chỉ là một yếu tố trong tử vi, nhưng nó cung cấp thông tin quan trọng về tính cách và khả năng của người sinh năm 1968. Từ đó, gia chủ có thể sử dụng thông tin này để tìm hiểu và ứng phó với các sự kiện trong cuộc sống một cách tốt nhất.
5. Tính cách nữ Mậu Thân 1968
Người sinh năm Mậu Thân 1968, bất kể là nam hay nữ đều được biết đến với trí thông minh và tài năng đáng nể. Đặc biệt, họ có niềm đam mê tìm hiểu và học hỏi về những điều mới. Tài năng tiếp thu nhanh chóng và sự nhạy bén trong mọi lĩnh vực là những đặc điểm nổi bật của họ.

1968 bao nhiêu tuổi năm 2023
Phụ nữ sinh năm 1968 có tính cách kiên định và lập trường vững vàng. Họ tự mình hình thành quan điểm và giữ vững lập trường của mình, bất chấp những tác động bên ngoài. Tuy nhiên, sự kiên định quá mức có thể đem lại một số khó khăn trong cuộc sống. Mặc dù phụ nữ sinh năm Mậu Thân 1968 rất lương thiện và tốt bụng nhưng họ không giỏi trong việc thể hiện điều đó ra bên ngoài.
Từ đó, họ có thể gặp hiểu lầm trong các mối quan hệ và gặp khó khăn trong việc thu hút sự thiện cảm từ người khác.
6. Tính cách nam Mậu Thân 1968
Nam sinh năm Mậu Thân 1968 được biết đến với sự thông minh, khéo léo và khiếu hài hước. Tính tò mò trong họ luôn thúc đẩy họ khám phá những điều mới mẻ trong cuộc sống. Họ luôn thích tạo tiếng cười nhưng đôi khi việc này có thể gây tổn thương cho người khác khi trò đùa đi quá giới hạn.

1969 tuổi gì bao nhiêu tuổi
Mặc dù rất thông minh, sắc bén nhưng nam Thân 1968 có thể trở nên cứng đầu và không muốn lắng nghe ý kiến của người khác. Đôi khi, họ cũng có thể thiếu trưởng thành trong những quyết định và họ có xu hướng không chia sẻ cảm xúc của mình với người khác.
7. Sinh năm 1968 hợp con số nào?
Bên cạnh việc tìm hiểu sinh năm 1968 bao nhiêu tuổi gì những con số hợp mệnh dưới đây cũng sẽ đem lại vô vàn điều may mắn cho Mậu Thân 1968.
Người sinh năm 1968, đặc biệt là nam và nữ tuổi Mậu Thân, có thể lựa chọn những con số may mắn phù hợp với bản mệnh của mình. Cụ thể:
- Nam sinh năm 1968: Gia chủ nam tuổi Mậu Thân hợp với số 5. Chọn số 5 làm con số chủ đạo trong cuộc sống hàng ngày có thể mang lại nhiều may mắn và thành công trong sự nghiệp. Con số 5 liên quan đến sự tự do, sáng tạo và cuộc sống đa dạng. Gia chủ nam có thể tận dụng số 5 để thúc đẩy sự phát triển cá nhân, thành công trong học tập, thi cử và đạt được những kết quả cao.

Số 5 hợp với Mậu Thân
- Nữ sinh năm 1968: Gia chủ nữ tuổi Mậu Thân hợp với số 1. Chọn số 1 làm con số chủ đạo trong cuộc sống có thể mang lại nhiều tình yêu thương từ mọi người xung quanh và quý nhân phù trợ giúp đỡ trong cuộc sống và sự nghiệp. Con số 1 thường liên quan đến sự lãnh đạo, độc lập và quyết tâm. Gia chủ nữ có thể tận dụng số 1 để thể hiện sự mạnh mẽ, khéo léo trong việc đạt được mục tiêu và thu hút sự ủng hộ và đồng lòng từ người khác.
Lựa chọn con số phù hợp với bản mệnh là một trong những cách để gia chủ tạo điều kiện thuận lợi, tránh khỏi điều không may và tận hưởng những cơ hội may mắn trong cuộc sống. Tuy nhiên, nên nhớ rằng con số may mắn chỉ là một yếu tố nhỏ trong tổng thể tử vi và phong thủy, và việc đạt thành công và hạnh phúc phụ thuộc vào nhiều yếu tố khác nhau.
8. Sinh năm 1968 hợp, kỵ hướng nào?
Vậy sinh năm 1968 mạng gì, hợp và kỵ dưới nào?
Người sinh năm 1968 cầm tinh con Khỉ được mô tả là những người thông minh, nhanh nhẹn và tài giỏi trong cuộc sống. Họ có tầm nhìn xa trông rộng và dễ dàng tìm kiếm nhiều cơ hội tốt cho bản thân. Tuy nhiên, vận mệnh của họ thường gặp nhiều khó khăn, đặc biệt là về vấn đề kinh tế. Đó là lý do tại sao, để tận hưởng cuộc sống hạnh phúc và đạt được sự ổn định kinh tế, người tuổi Mậu Thân cần chú trọng đến hướng xuất hành và hướng nhà hợp phong thủy để thu hút tài lộc và xua đuổi vận xui cho cả gia đình.
Vậy, không chỉ quan tâm đến mệnh số, mà còn phải tìm hiểu hướng phù hợp cho người sinh năm 1968. Nam sinh năm này thì hợp với các hướng Tây Bắc, Tây Nam, Đông Bắc và Tây, trong khi đó nữ sinh năm 1968 hợp với các hướng Nam, Bắc, Đông và Đông Bắc. Chọn đúng hướng phù hợp sẽ mang lại nhiều may mắn, gia đình sung túc và sự hòa hợp.
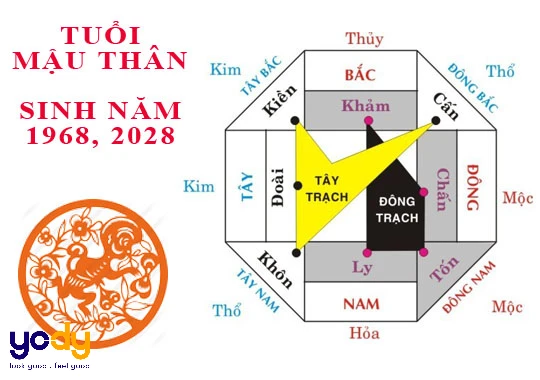
Hướng nào phù hợp với tuổi 1968
Ngoài ra, cũng cần lưu ý đến các hướng phòng trong nhà. Hướng bếp nên chọn các hướng Bắc, Đông, Nam và Đông Nam để đẩy lùi tà khí. Phòng ngủ, một không gian để nghỉ ngơi và tái tạo năng lượng, nên có hướng Tây, Tây Nam, Tây Bắc và Đông Bắc cho nam sinh năm 1968, trong khi nữ sinh năm 1968 nên chọn hướng Đông, Đông Nam, Nam và Bắc. Phòng thờ, nơi linh thiêng để thể hiện lòng thành kính đối với tổ tiên, cần có hướng cát thuộc các cung Diên Niên, Sinh Khí, Thiên Y và Phục Vị. Đối với nữ sinh năm 1968, các hướng tốt cho bàn thờ là Đông Nam, Đông, Nam và Bắc, trong khi nam sinh năm 1968 nên chọn hướng Tây Nam, Tây Bắc và Đông Nam.
9. Tuổi 1968 hợp với các tuổi nào?
Khi tìm hiểu về mệnh số của nam Mậu Thân 1968 và nữ Mậu Thân 1968, có một yếu tố quan trọng cần xem xét là các tuổi hợp và kỵ trong việc hợp tác kinh doanh, kết hôn và xây dựng gia đình. Điều này có ý nghĩa đặc biệt quan trọng và ảnh hưởng lớn đến cuộc sống của gia chủ trong tương lai. Do đó, để đạt được sự thuận lợi trong sự nghiệp và sự hòa hợp trong gia đình, khách hàng nên tránh kết hôn với người có tuổi trái ngược.
Dưới đây là một số tuổi hợp và kỵ cho nam Mậu Thân 1968 và nữ Mậu Thân 1968:
Nam Mậu Thân 1968:
- Tuổi hợp kinh doanh: Kỷ Dậu, Ất Mão, Quý Sửu
- Tuổi hợp vợ chồng: Nữ sinh năm 1965, 1956, 1955, 1964 và 1963
- Tuổi kỵ: Tân Hợi, Quý Hợi

Kỷ Dậu phù hợp với 1968
Nữ Mậu Thân 1968:
- Tuổi hợp kinh doanh: Tương tự như nam sinh năm 1968: Kỷ Dậu, Ất Mão, Quý Sửu
- Tuổi hợp vợ chồng: Nam sinh năm 1968, 1970, 1978 và 1969
- Tuổi kỵ: Tân Hợi, Quý Hợi
10. Tính cách của những người sinh năm 1968
Những người sinh năm tuổi Thân 1968 có tính cách đặc biệt. Họ được cho là thông minh và tinh tế trong suy nghĩ, đồng thời mang trong mình một tinh thần tự do và phóng khoáng. Sự thông minh và khả năng nắm bắt nhanh chóng giúp họ vượt qua các thử thách trong cuộc sống một cách dễ dàng.
Người sinh năm Mậu Thân 1968 có trái tim ấm áp và luôn sẵn lòng giúp đỡ người khác. Họ có lòng yêu thương và quan tâm đến mọi người xung quanh, và luôn cố gắng hỗ trợ mọi người trong khả năng của mình. Mặc dù họ có tình cảm sâu sắc và tốt bụng, nhưng thường họ không thể hiện nhiều ra bên ngoài và giữ cho mình những cảm xúc sâu thẳm.

Tính cách của những người 1986
Đặc biệt, những người sinh năm Mậu Thân 1968 thường rất kiên nhẫn và kiên định. Dù gặp khó khăn và trở ngại, họ không bao giờ chịu lòng dễ dàng. Sự bền bỉ và kiên trì giúp họ vượt qua mọi thử thách và đạt được thành công trong sự nghiệp. Họ cũng có xu hướng làm việc chăm chỉ, đặt mục tiêu cao và luôn tìm kiếm những cách sáng tạo để tiến xa hơn trong cuộc sống.
11. Vật phẩm hộ mệnh của tuổi Mậu Thân 1968
Không chỉ tìm hiểu tuổi Mậu Thân mạng gì mà trang bị các vật phẩm hộ mệnh cũng đem lại vô vàn điều may mắn, tài lộc cho tuổi này.
Các vật phẩm phong thủy được đề cập có thể mang lại tài lộc và may mắn cho người tuổi Mậu Thân 1968. Dưới đây là mô tả về mỗi vật phẩm:
- Gậy Như Ý: Biểu tượng của quyền lực và sức mạnh, giúp chủ nhân thuận buồm xuôi gió trong công việc và đạt được những ước muốn.
- Tượng phật Di Lặc: Được xem là biểu tượng của sự sung túc và may mắn, mang lại tài lộc cho chủ nhân.
- Quả cầu phong thủy: Một món đồ thu hút năng lượng tích cực và vượng khí, giúp hấp dẫn tài lộc và sự thành công.
- Thiềm thừ: Hình ảnh con cóc ngậm đồng xu, biểu tượng của tài lộc và may mắn, giúp thu hút những điều tốt lành.
- Tỳ hưu: Tượng tượng trưng cho may mắn và hạnh phúc, giúp xua đuổi tà khí và mang lại sự thịnh vượng.

Tỳ Hưu là vật phẩm phù hợp
- Phật bà Quan âm ngọc Hoàng Long: Tượng Phật bà Quan âm giúp giải trừ những điều không may, biểu tượng của sự tốt lành và bình an.
- Đá cảnh Thạch Anh hồng: Được làm từ đá thạch anh, giúp tăng cường sự lưu thông của máu huyết và mang đến năng lượng tích cực cho chủ nhân.
- Tượng ngựa giương vó: Phù hợp cho những người làm ăn kinh doanh, biểu tượng cho sự phát triển sự nghiệp và cuộc sống thịnh vượng.
- Tượng trâu: Biểu tượng sự chăm chỉ và cống hiến, mang ý nghĩa thịnh vượng và thành công.
- Kim Nguyên Bảo Ngọc Hoàng: Vật phẩm mang ý nghĩa giàu sang, tiền tài, sung túc và thành công trong cuộc sống kinh doanh.
Lưu ý rằng phong thủy chỉ là một yếu tố tương đối và không thay thế cho việc nỗ lực, cố gắng và khả năng cá nhân. Tuy nhiên, nếu bạn tin vào sự ảnh hưởng của phong thủy, các vật phẩm này có thể tạo ra một môi trường tích cực và hỗ trợ trong cuộc sống của bạn.
12. 1968 bao nhiêu tuổi?
Năm 1968 đã trôi qua một quãng đường dài, và giờ đây nó đã trở thành một kỷ niệm sống động trong lòng những người sinh vào năm đó. Với 55 năm trôi qua, những người tuổi Mậu Thân 1968 đã trải qua nhiều khó khăn, thử thách và thành công trong cuộc sống.
55 tuổi - một tuổi tác đáng trân trọng và đáng tự hào. Đó là thời điểm mà con người trở nên tự tin, sáng suốt hơn về những gì mình đã đạt được và những gì mình muốn trong tương lai. Đây cũng là thời điểm để nhìn lại quá khứ với sự biết ơn và sẵn sàng đón nhận những thách thức mới.
Với 55 năm tuổi, những người sinh năm 1968 mang trong mình sự trưởng thành và sự hiểu biết sâu sắc về cuộc sống. Họ đã trải qua nhiều giai đoạn khác nhau, từ tuổi trẻ đầy nhiệt huyết đến tuổi trung niên đầy trách nhiệm. Những trải nghiệm, hành trình và sự tự tìm kiếm đã giúp họ phát triển thành những con người đa tài và sáng tạo.
Hy vọng, với bài viết về 1968 mệnh gì mà YODY vừa gửi đến các bạn cũng đã có thêm nhiều thông tin hữu ích dành cho mình.
Link nội dung: https://getairvestal.com/1968-menh-gi-hop-tuoi-nao-huong-nao-xem-phong-thuy-1968-a12178.html