Chứng minh ba đường thẳng đồng quy trong không gian - O₂ Education

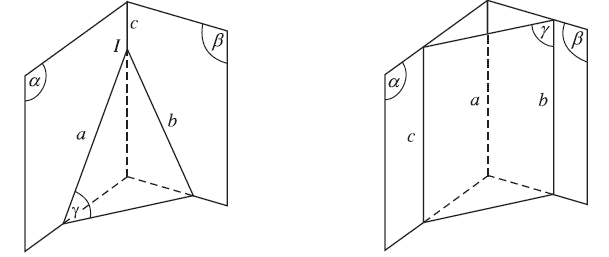
Nhờ việc sử dụng định lí về giao tuyến của ba mặt phẳng phân biệt trong không gian hoặc đồng quy, hoặc đôi một so sánh nên trong không gian để chứng minh ba đường thẳng a, b, c đồng quy ta có thể làm như sau:

• Tìm giao điểm I của hai trong ba đường thẳng đã cho, chẳng hạn a và b;
• Giả sử c là giao tuyến của hai mặt phẳng (α) và (β) nào đó lần lượt chứa đường thẳng a và đường thẳng b;
• Chứng minh rằng I là điểm chung của (α) và (β), tức là I phải thuộc vào giao tuyến c;
• Kết luận: a, b, c đồng quy tại O.

Xem thêm Cách chứng minh thẳng hàng trong hình học không gian

Ví dụ. Cho tứ diện ABCD. Gọi M; N lần lượt là trung điểm của AB và CD. Mặt phẳng (P) qua MN và cắt AD; BC lần lượt tại P và Q. Biết MP cắt NQ tại I. Chứng minh rằng MP, NQ và BD đồng quy tại I.

Lời giải

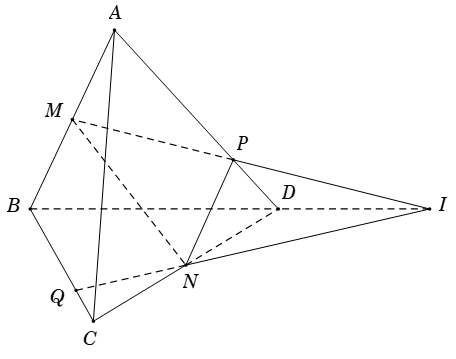
Ta có: (ABD) ∩ (BCD) = BD

Lại có I ∈ MP ⊂ (ABD) và I ∈ NQ ⊂ (BCD) nên I là điểm chung của hai mặt phẳng (ABD) và (BCD). Nói cách khác, I thuộc vào giao tuyến của hai mặt phẳng (ABD) và (BCD).

Do đó, I ∈ BD hay ba đường thẳng MP, NQ và BD đồng quy tại I.

Bài 1. Cho tứ diện ABCD mặt phẳng(P) không chứa AB và CD cắt các cạnh AC, BC, AD lần lượt tại M, N, R, S.

1. Chứng minh 3 đường thẳng AB, MN, RS đồng qui.
2. Chứng minh 3 đường thẳng CD, MS, NR đồng qui

Bài 2. Cho tứ diện ABCD. M, N lần lượt là trung điểm BC, BD. Các điểm P và S lần lượt thuộc AD, AC sao cho AR= AD:3 ; AS= AC:3. CMR ba đường thẳng AB, MS, NR đồng qui.

Bài 3. Cho hình thang ABCD (AB// CD) điểm S nằm ngoài mặt phẳng chứa ABCD. Gọi M, N lần lượt là trung điểm của SC, SD. Gọi I là giao điểm của AD và BC, J là giao điểm của AN và BM. Gọi O là giao điểm của AC và BD. CMR : SO, AM, BN đồng qui.