19/10/2024 15:55

In bài này (Ctrl+P)

Hình thoi và hình vuông |Toán 8 chương trình mới

1. Hình thoi

- Khái niệm: Hình thoi là tứ giác có bốn cạnh bằng nhau.

- Tính chất: Trong hình thoi:

+ Hai đường chéo vuông góc với nhau;

+ Hai đường chéo là các đường phân giác của các góc trong hình thoi.

- Dấu hiệu nhận biết:

+ Hình bình hành có hai cạnh kề bằng nhau là hình thoi.

+ Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

+ Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

2. Hình vuông

- Khái niệm: Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.

- Tính chất: Trong một hình vuông, hai đường chéo bằng nhau, vuông góc với nhau, cắt nhau tại trung điểm của mỗi đường và là các đường phân giác của các góc của hình vuông.

- Dấu hiệu nhận biết:

+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

+ Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.

>> Xem thêm: Tổng hợp kiến thức toán 8 chi tiết SGK mới

3. Bài tập hình thoi và hình vuông toán 8 chương trình mới

3.1 Bài tập hình thoi và hình vuông toán 8 kết nối tri thức

Bài 3.30 trang 72 SGK toán 8/1 kết nối tri thức

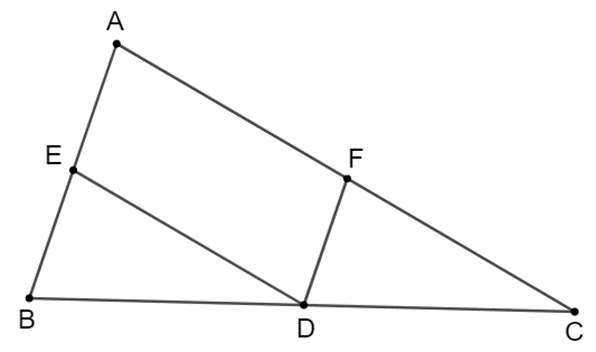
Hình thoi và hình vuông |Toán 8 chương trình mới

a) Tứ giác AEDF có AE // DF; AF // DE (giả thiết).

=> tứ giác AEDF là hình bình hành.

b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A.

Mà $\large \Delta$ ABC cân tại A nên đường phân giác AD đồng thời là đường trung tuyến

Do đó D là trung điểm của BC.

Ngược lại, nếu D là trung điểm của cạnh BC của $\large \Delta$ ABC cân tại A thì hình bình hành AEDF có đường chéo AD là đường phân giác của góc A nên AEDF là hình thoi.

c) Nếu $\large \Delta$ ABC vuông tại A thì AEDF là hình chữ nhật (vì hình bình hành có một góc vuông là hình chữ nhật).

d) $\large \Delta$ ABC vuông cân tại A tức là vừa vuông tại A vừa cân tại A.

Theo câu c, nếu $\large \Delta$ ABC vuông tại A thì AEDF là hình chữ nhật.

Để hình chữ nhật AEDF là hình vuông thì tức nó cũng là hình thoi.

Theo câu b, AEDF là hình thoi nếu D là trung điểm của cạnh BC của tam giác ABC cân tại A.

Vậy nếu tam giác ABC vuông cân tại A thì để AEDF là hình vuông thì điểm D là trung điểm của BC.

Bài 3.31 trang 72 SGK toán 8/1 kết nối tri thức

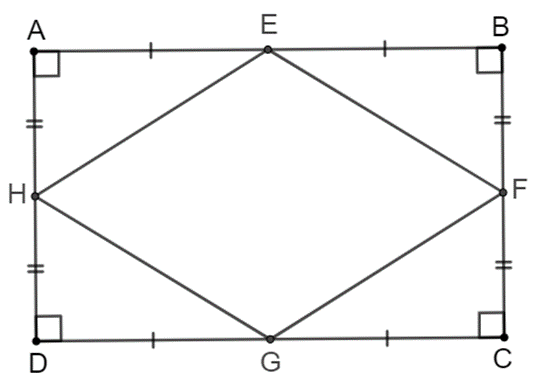
Hình thoi và hình vuông |Toán 8 chương trình mới

Ta cần chứng minh EFGH là hình thoi. Thật vậy:

Do ABCD là hình chữ nhật nên AD = BC.

H là trung điểm của AD nên AH = DH = 1/2 AD ;

F là trung điểm của BC nên BF = CF = 1/2 BC

Do đó AH = DH = BF = CF.

Xét $\large \Delta$ AHE và $\large \Delta$ BFE có:

$\large \widehat{HAE}=\widehat{FBE}$ = 90°;

AE = BE (do E là trung điểm của AB);

AH = BF (chứng minh trên).

Do đó $\large \Delta$ AHE = $\large \Delta$ BFE (hai cạnh góc vuông)

=> HE = FE (hai cạnh tương ứng).

Tương tự, ta cũng có:

• $\large \Delta$ BEF = $\large \Delta$ CGF (hai cạnh góc vuông) => EF = GF (hai cạnh tương ứng).

• $\large \Delta$ CGF = $\large \Delta$ DGH (hai cạnh góc vuông), => GF = GH (hai cạnh tương ứng).

Từ đó ta có EF = FG = GH = HE

Do đó tứ giác EFHG là hình thoi.

Bài 3.32 trang 72 SGK toán 8/1 kết nối tri thức

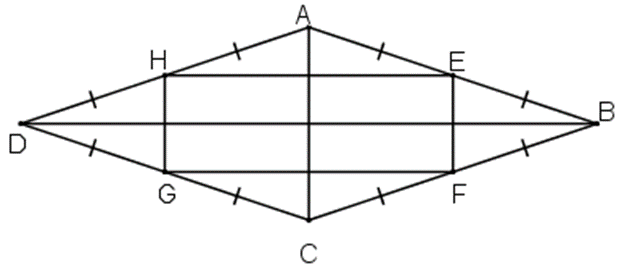
Hình thoi và hình vuông |Toán 8 chương trình mới

Ta cần chứng minh EFGH là hình chữ nhật. Thật vậy:

Do ABCD là hình thoi nên AB = BC = CD = DA.

Do E, H lần lượt là trung điểm của AB, AD nên AH = DH = AE = BE.

Tam giác AHE có AH = AE nên là tam giác cân tại A

$\large \Rightarrow \widehat{AHE}=\widehat{AEH}$

Mà $\large \widehat{HAE}+\widehat{AHE}+\widehat{AEH}=180^{o}$

$\large \Rightarrow \widehat{AHE}=\frac{180^{o}-\widehat{HAE}}{2}$

Tương tự, ta có tam giác DHG cân tại D

$\large \Rightarrow \widehat{DHG}=\frac{180^{o}-\widehat{HDG}}{2}$

Mặt khác, do ABCD là hình thoi nên AB // CD

$\large \Rightarrow \widehat{HAE}+\widehat{HDG}=180^{o}$

$\large \Rightarrow \widehat{AHE} + \widehat{DHG}=\frac{180^{o}-\widehat{HAE}}{2}+\frac{180^{o}-\widehat{HDG}}{2}$

$\large =\frac{180^{o}-\widehat{HAE}+180^{o}-\widehat{HDG}}{2}=\frac{360^{o}-180^{o}}{2}=90^{o}$

Mà $\large \widehat{EHG}=180^{o}-(\widehat{AHE}+\widehat{DHG})=180^{o}-90^{o}=90^{o}$

Chứng minh tương tự ta có: $\large \widehat{HEF}=\widehat{EFG}=\widehat{FGH}=90^{o}$

Tứ giác EFGH có bốn góc vuông nên là hình chữ nhật.

Bài 3.33 trang 72 SGK toán 8/1 kết nối tri thức

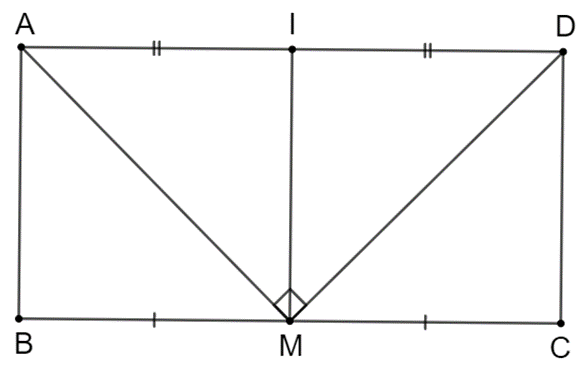
Hình thoi và hình vuông |Toán 8 chương trình mới

Gọi I là trung điểm của AD.

Khi đó, MI = AD/2 mà M là trung điểm của BC nên MI = AB.

Suy ra AB = AD/2 nên AD = 2AB.

Mà AB + AD = 36/2 = 18 (cm).

Suy ra AB + 2AB = 18

Hay 3AB = 18

Do đó AB = 6 (cm).

Suy ra AD = 2AB = 2 . 6 = 12 (cm).

Vậy độ dài các cạnh của hình chữ nhật ABCD là AB = CD = 6 cm; AD = BC = 12 cm.

Duy nhất khóa học DUO tại VUIHOC dành riêng cho cấp THCS, các em sẽ được học tập cùng các thầy cô đến từ top 5 trường chuyên toàn quốc. Nhanh tay đăng ký thôi !!!!

Hình thoi và hình vuông |Toán 8 chương trình mới

3.2 Bài tập hình thoi và hình vuông toán 8 chân trời sáng tạo

Bài 6 trang 81 Toán 8/1 Chân trời sáng tạo

Ta có AE = EB nên AB = 2AE.

DG = GC nên DC = 2DG.

Mà AE = DG nên AB = DC.

Chứng minh tương tự ta cũng có: AD = BC.

Tứ giác ABCD có AB = DC và AD = BC nên là hình bình hành (dấu hiệu nhận biết).

Suy ra AB // CD và AD // BC.

Lại có AD ⊥ AB nên AD ⊥ CD; AB ⊥ BC; BC ⊥ CD.

Xét DAEH và DBEF có:

$\large \widehat{EAH}=\widehat{EBF}$ = 90°; AE = BE; AH = BF.

Do đó DAEH = DBEF (hai cạnh góc vuông).

Suy ra HE = FE (hai cạnh tương ứng).

Chứng minh tương tự ta cũng có: HE = HG; HE = FG.

Do đó HE = EF = FG = GH.

Tứ giác EFGH có HE = EF = FG = GH nên là hình thoi.

Bài 7 trang 81 Toán 8/1 Chân trời sáng tạo

Do ABCD là hình thoi nên hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường.

Do đó OA= 1/2AC = 3(cm) và OB=1/2BD = 4(cm).

Áp dụng định lí Pythagore vào DOAB vuông tại O, ta có:

AB2 = OA2 + OB2

$\large \Rightarrow AB=\sqrt{OA^{2}+OB^{2}}=\sqrt{3^{2}+4^{2}}=5cm$

Bài 8 trang 81 Toán 8/1 Chân trời sáng tạo

a) Ta có A đối xứng với D qua BC nên M là trung điểm của AD và BC ⊥ AD.

Tứ giác ABDC có hai đường chéo AD và BD cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.

Lại có hai đường chéo AD ⊥ BC => ABDC là hình thoi.

b) Ta có E là trung điểm của OM và AB nên hai đường chéo của tứ giác OAMB cắt nhau tại trung điểm của mỗi đường.

Do đó tứ giác OAMB là hình bình hành.

=> OA // BM và OB // AM.

Ta có OB // AM và AM ⊥ BM nên OB ⊥ BM, do đó DMBO vuông tại B.

Ta có OA // BM và OB ⊥ BM nên OA ⊥ OB, do đó DAOB vuông tại O.

Do OAMB là hình bình hành nên OA = BM và OB = AM.

Xét DMBO vuông tại B và DAOB vuông tại O có:

OB = AM; BM = OA

Do đó DMBO = DAOB (hai cạnh góc vuông).

3.3 Bài tập hình thoi và hình vuông toán 8 cánh diều

Bài 1 trang 115 toán 8/1 cánh diều

Do AC là tia phân giác của góc DAB nên $\large \widehat{BAC}=\widehat{DAC}$ .

Mặt khác do ABCD là hình bình hành nên AB // CD

$\large \Rightarrow \widehat{BAC}=\widehat{DCA}$ (so le trong).

Do đó $\large \widehat{DAC}=\widehat{DCA}$

Xét $\large \Delta$ DAC có $\large \widehat{DAC}\widehat{DCA}$ nên $\large \Delta$ DAC cân tại D .

=> DA = DC.

Hình bình hành ABCD có hai cạnh kề DA và DC bằng nhau nên là hình thoi.

Bài 2 trang 115 toán 8/1 cánh diều

Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường.

Do đó AC = 2OA, BD = 2OB.

Ta có: AC2 + BD2 = (2OA)2 + (2OB)2 = 4OA2 + 4OB2 = 4(OA2 + OB2).

Xét ΔOAB vuông tại O, theo định lí Pythagore ta có:

AB2 = OA2 + OB2

Suy ra AC2 + BD2 = 4(OA2 + OB2) = 4AB2.

Bài 3 trang 115 toán 8/1 cánh diều

Vì ABCD là hình thoi nên BD là phân giác của $\large \widehat{ADC}$

Do đó $\large \widehat{ADC}=2\widehat{CDB}=2.40^{o}=80^{o}$

$\large \Rightarrow \widehat{ABC}=\widehat{ADC}=80^{o}$

Do ABCD là hình thoi nên AB // CD, do đó $\large \widehat{BAD}=\widehat{ADC}=180^{o}$

$\large \Rightarrow \widehat{BAD}=180^{o}-\widehat{ADC}=180^{o}-80^{o}=100^{o}$

Do đó $\large \widehat{BCD}=\widehat{BAD}=100^{o}$

Vậy $\large \widehat{ABC}=\widehat{ADC}=80^{o} ; \widehat{BCD}=\widehat{BAD}=100^{o}$

Bài 4 trang 115 toán 8/1 cánh diều

Giả sử một lưới mắt cáo được mô tả bởi hình thoi ABCD như hình vẽ trên.

Khi đó AC = 90 mm, BD = 45 mm.

Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường.

Suy ra OA=1/2AC = 45(mm); OB=1/2BD = 22,5(mm).

Xét $\large \Delta$ OAB vuông tại O, theo định lí Pythagore ta có:

AB2 = OA2 + OB2 = 452 + 22,52 = 2 025 + 506,25 = 2531,25

$\large \Rightarrow AB=\sqrt{2531,25}\approx 50mm$

Bài 5 trang 115 toán 8/1 cánh diều

Giả sử viên gạch trang trí được mô tả bởi hình thoi ABCD như hình vẽ trên với $\large \widehat{BCD}=60^{o}$

• Tam giác BCD có BC = CD (do ABCD là hình thoi) nên là tam giác cân tại C.

Lại có $\large \widehat{BCD}=60^{o}$ nên $\large \Delta$ BCD là tam giác đều.

Do đó BC = CD = BD = 40 cm.

• Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường.

Suy ra OB=1/2BD = 20(cm)

Xét $\large \Delta$ OBC vuông tại O, theo định lí Pythagore ta có:

BC2 = OB2 + OC2

Do đó OC2 = BC2 - OB2 = 402 - 202 = 1600 - 400 = 1200.

$\large \Rightarrow OC=\sqrt{1200}\approx 34,64cm$

Mà O là trung điểm của AC nên AC = 2OC ≈ 69,28 (cm).

• Diện tích của viên gạch có dạng hình thoi đó là:

$\large S_{ABCD}=\frac{1}{2}AC.BD\approx \frac{1}{2}69,28.80=2771,2cm^{2}$

Trên đây là những kiến thức về hình thoi và hình vuông trong chương trình toán 8 kết nối tri thức, chân trời sáng tạo và cánh diều. Bên cạnh đó VUIHOC hướng dẫn các em cách giải các bài tập trong sách giáo khoa. Truy cập vuihoc.vn để cập nhật thêm nhiều kiến thức toán 8 bổ ích nhé các em!

>> Mời bạn tham khảo thêm:

Hình thang cân
Hình bình hành
Hình chữ nhật

Link nội dung: https://getairvestal.com/hinh-thoi-va-hinh-vuong-toan-8-chuong-trinh-moi-a15486.html