Cách Chứng Minh Hai Mặt Phẳng Song Song Và Bài Tập Minh Họa

1. Lý thuyết về hai mặt phẳng song song

1.1. Thế nào là hai mặt phẳng song song?

Để có thể chứng minh hai mặt phẳng song song với nhau, chúng ta cần phải nắm chắc khái niệm thế nào là hai mặt phẳng song song. Trong không gian, hai mặt phẳng được gọi là song song với nhau khi giữa chúng không có điểm chung nào.

1.2. Định lý về 2 mặt phẳng song song

Trong không gian, nếu mặt phẳng (α) chứa 2 đường thẳng cùng song song với mặt phẳng (β) và 2 đường thẳng cắt nhau a, b thì mặt phẳng (α) song song với mặt phẳng (β).

1.3. Các tính chất của hai mặt phẳng song song

Khi qua điểm nằm ngoài mặt phẳng cho trước chỉ một và một mặt phẳng song song với mặt phẳng đề bài đã cho

• Hệ quả 1: Nếu đường thẳng d song song với (α) thì qua d có duy nhất 1 mặt phẳng song song với mặt phẳng (α).

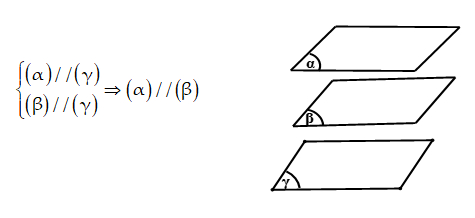
• Hệ quả 2: Hai mặt phẳng phân biệt với nhau cùng song song với mặt phẳng thứ 3 thì song song nhau.

• Hệ quả 3: Cho điểm A không nằm trên (α). Mọi đường thẳng đi qua A và song song với mặt phẳng (α) đều nằm trong mặt phẳng đi qua A và song song với (α).

Ta có 2 mặt phẳng song song nhau. Nếu 1 mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song nhau.

1.4. Hình lăng trụ và hình hộp

Hình lăng trụ là hình đa diện có hai mặt nằm bên trong. Hình lăng trụ gồm có 2 đáy là 2 đa giác bằng nhau và nằm trên hai mặt phẳng song song, các mặt bên là hình bình hành, các cạnh bên bằng nhau hoặc song song với nhau.

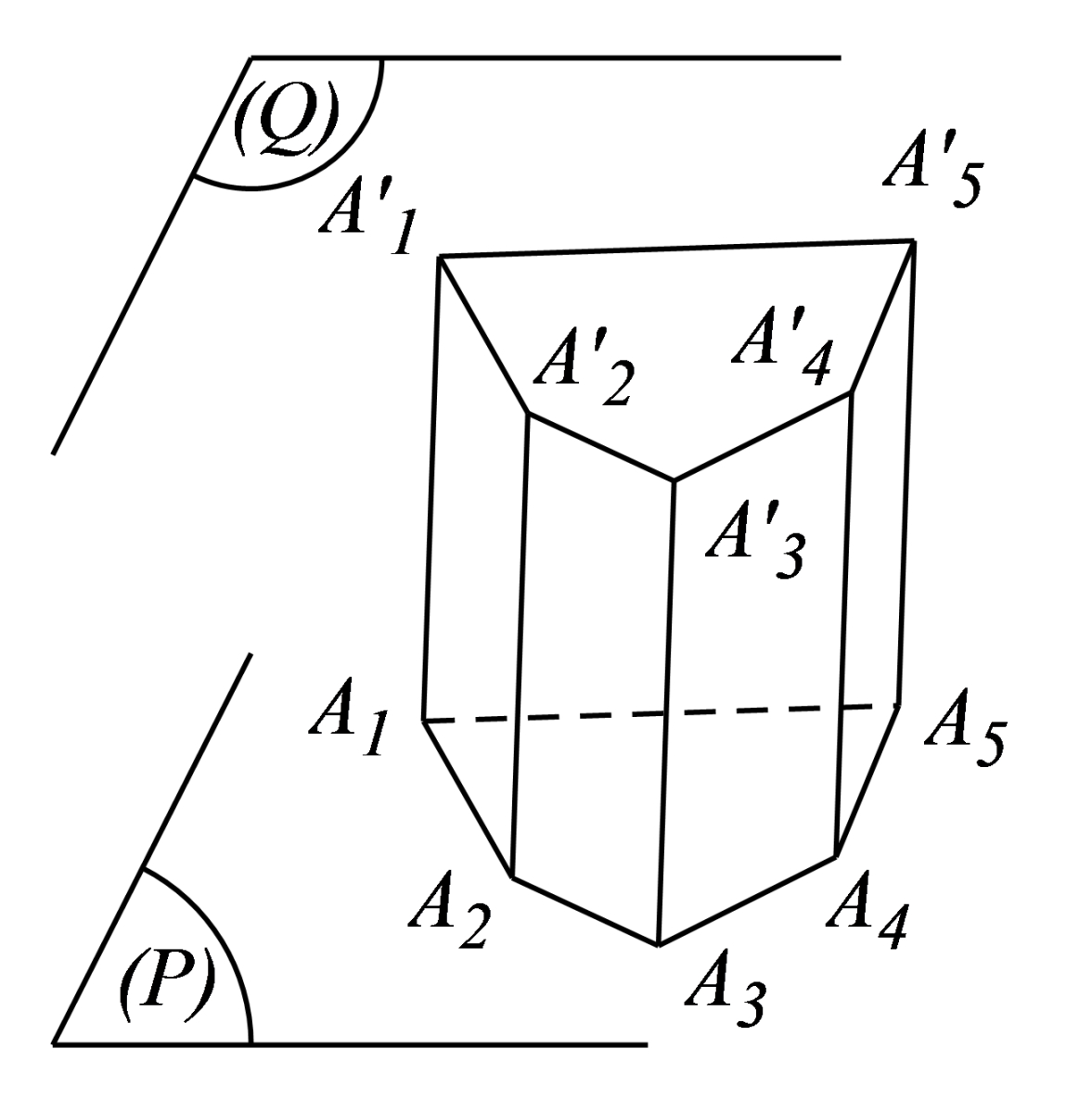
Hình lăng trụ có những tính chất như:

• Các cạnh bên bằng nhau với nhau và song song nhau.

• Các mặt bên và các mặt chéo là hình bình hành.

• Có 2 đáy là đa giác có các cạnh song song nhau, bằng nhau.

Một hình lăng trụ có đáy là hình bình hành sẽ được gọi là hình hộp.

Hình hộp có tất cả các mặt đáy và các mặt bên đều là hình chữ nhật sẽ được gọi là hình hộp chữ nhật.

Hình hộp có tất cả các mặt bên là hình vuông được gọi là hình lập phương.

1.5. Hình chóp cụt

Hình chóp cụt là hình có phần chóp nằm giữa đáy và thiết diện cắt bởi mặt phẳng song song với đáy hình chóp.

Hình chóp cụt là hình có các tính chất:

• 2 đáy là đa giác có tỉ số các cạnh tương ứng bằng nhau và các cạnh tương ứng song song với nhau.

• Các mặt bên là hình thang.

• Có các đường thẳng chứa cạnh bên đồng quy tại 1 điểm.

2. Các cách chứng minh hai mặt phẳng song song

Cách chứng minh hai mặt phẳng song song với nhau được làm theo các cách như sau, các bạn học sinh hãy theo dõi nhé!

2.1. Chứng minh mặt phẳng này chứa hai đường thẳng cắt nhau cùng song song với mặt phẳng kia

2.2. Phương pháp chứng minh 2 mặt phẳng đó cùng song song với mặt phẳng thứ ba

3. Ví dụ vận dụng phương pháp chứng minh hai mặt phẳng song song

Chúng ta đã biết cách chứng minh hai mặt phẳng song song. Để hiểu rõ hơn về bài tập này, các bạn học sinh cùng luyện tập một số ví dụ sau đây:

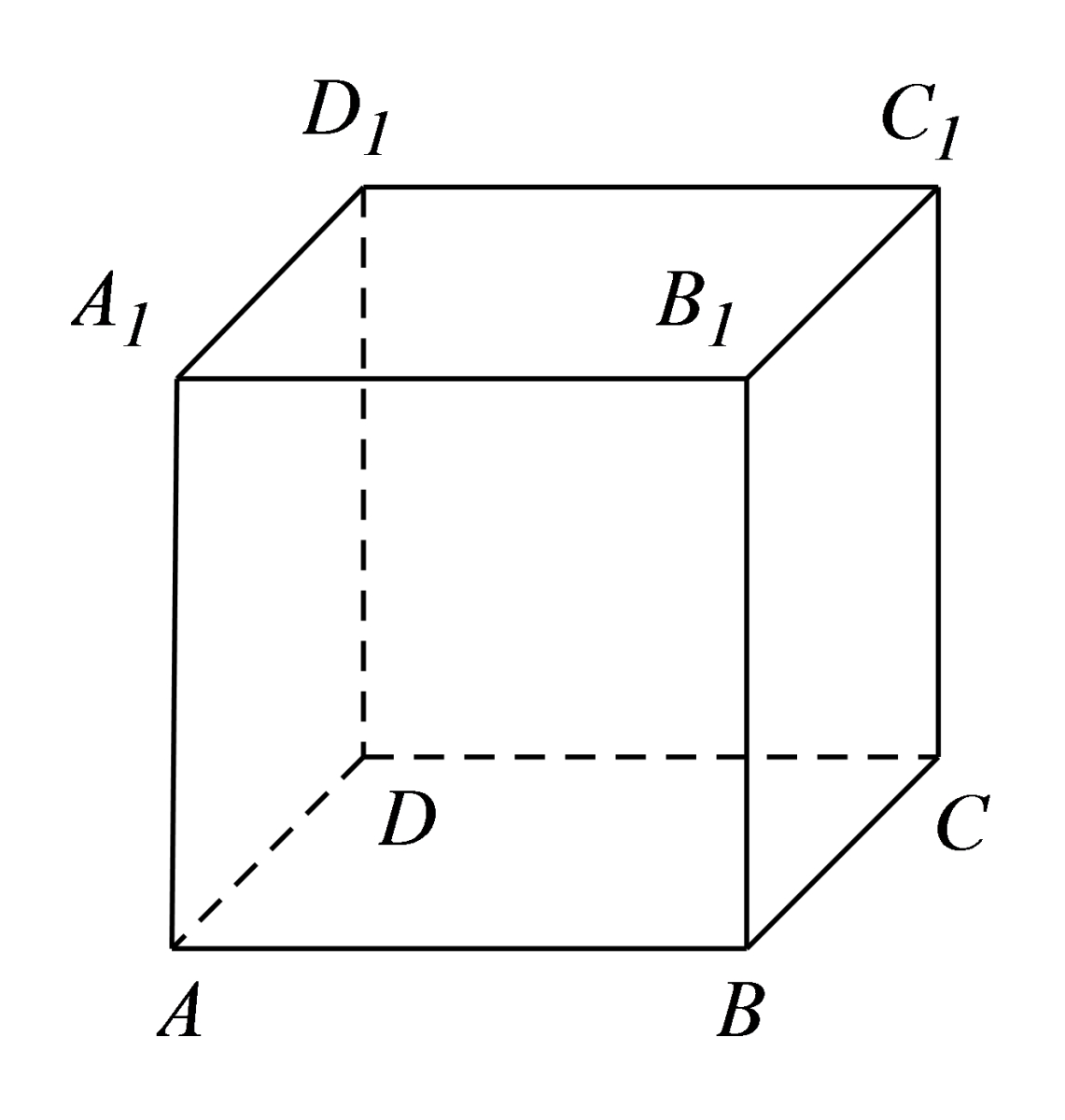
Bài 1: Cho hình hộp ABCD.A’B’C’D’. Hãy cho biết mặt phẳng (AB’D’) song song với mặt phẳng nào?

Giải:

Do BDD’B’ là hình bình hành $\Rightarrow$ BD // B’D’ (1)

ADC’B’ là hình bình hành nên AB’ // DC’ (2)

(1) và (2) $\Rightarrow$ (AB’D’) // (BC’D)

Bài 2: Gọi M và N lần lượt là trung điểm của BB’ và CC’ của hình lăng trụ ABC.A’B’C’. Gọi Δ là một giao tuyến của 2 mặt phẳng (AMN) và (A’B’C’). Chứng minh rằng Δ // BC

Giải:

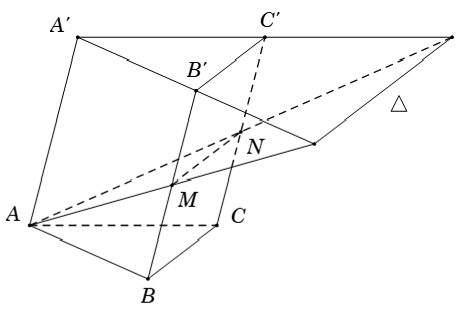
Ta có: MN ⊂ (AMN)

B'C' ⊂ (A'B'C')

MN // B'C'

⇒ Δ là giao tuyến của hai mặt phẳng (AMN) và (A’B’C’) song song với MN và B’C’

⇒ Δ // BC

Bài 3: Cho hai mặt phẳng song song với nhau α và β. Đường thẳng d nằm bên trong α. Vậy mặt phẳng d và β có điểm chung hay không?

Giải:

Hai mặt phẳng α và β song song ⇒ α và β không có điểm chung nào

d nằm bên trong mặt phẳng α

⇒ Đường thẳng d không cắt được mặt phẳng β. Vì khi d cắt mặt phẳng β tức là d và β có điểm chung

⇒ hai mặt phẳng α và β có điểm chung (mâu thuẫn giả thiết)

⇒ Mặt phẳng d và β không có điểm chung

Bài 4: Các bạn học sinh hãy tạo dựng mặt phẳng (α) qua trung điểm I của đoạn SA và song song với mặt phẳng (ABC) của tứ diện SABC.

Giải:

Mặt phẳng (α) đi qua 3 trung điểm I, L, K của SA, SC, SB

Do I, K, L là trung điểm của SA, SB, SC nên IK, KL cũng lần lượt là đường trung bình tam giác SAB và SBC.

IK song song AB ∈ (ABC) ⇒ IK // (ABC)

KL // BC ∈ (ABC) ⇒ KL // (ABC)

IK và KL cắt nhau và song song mặt phẳng (ABC)

⇒ Mặt phẳng có chứa đoạn IK và KL // (ABC) hay (α) // (ABC)

Bài 5: Mặt phẳng (α) có chứa hình bình hành ABCD. Qua các điểm A, B, C, D lần lượt vẽ đường thẳng a, b, c, d song song nhau và không nằm trên mặt phẳng (α). Trên a, b, c lấy ba điểm A’, B’ và C’ tùy ý. Xác định giao điểm D’ đường thẳng d với mặt phẳng (A’B’C’).

Giải:

Ví dụ mặt phẳng (A’B’C’) ∩ d = D’

⇒ (A’B’C’) ∩ (C’CD) = C’D’.

AA’ // CC’ ⊂ (C’CD)

⇒ AA’ // (C’CD).

AB // CD ⊂ (CC’D)

⇒ AB // (CC’D)

Mặt phẳng (AA’B’B) có

⇒ (AA’B’B) // (C’CD).

Ta lại có (A’B’C’) ∩ (AA’B’B) = A’B’

⇒ (A’B’C’) cắt (C’CD) và giao tuyến của chúng song song với A’B’

⇒ C’D’ // A’B’.

4. Bài tập chứng minh hai mặt phẳng song song

Bài tập chứng minh hai mặt phẳng song song sẽ giúp các em ôn tập thật tốt trong những bài kiểm tra hay các kỳ thi. Vì vậy đừng bỏ lỡ những bài tập dưới đây nhé.

Bài 1: Đáy ABCD là hình bình hành có tâm O của hình chóp S.ABCD. Gọi các điểm M, N, I là trung điểm của SA, SD và AB. Chứng minh (MON) // (SBC).

Giải:

Xét có: MN là một đường trung bình của tam giác SAD

$\Leftrightarrow$ MN // AD (1).

OP chính là đường trung bình của ABC

$\Rightarrow$ OP // BC // AD (2)

Từ (1) và (2): MN // OP // AD nên 4 điểm M; N; O; P đồng phẳng với nhau

Bài 2: Có điểm H là trung điểm của A’B’ hình lăng trụ ABC.A’B’C’. Mặt phẳng nào song song với đường thẳng B’C?

Giải:

Gọi M là trung điểm của AB:

⇒ AMB’H là hình bình hành

⇒ MB’//AH vậy MB’ // mặt phẳng (AHC’) (1)

Vì ta có MH là đường trung bình hình bình hành ABB’A’

⇒ MH song song và bằng BB’

⇒ MH song song và bằng CC’

⇒ MHC’C là hình bình hành

⇒ MC // HC’ vì vậy MC // (AHC’) (2)

Từ (1) và (2) ta có (B’MC) // (AHC’)

⇒ B’C // (AHC’)

Bài 3: Đáy ABCD là hình bình hành có tâm O của hình chóp S.ABCD. Gọi điểm M là trung điểm của SA, N là trung điểm của SD. Mệnh đề nào sau đây là sai?

A. OM // (SBC)

B. ON // (SAB)

C. (OMN) // (SBC)

D. (OMN) và (SBC) cắt nhau

Giải:

Ta gọi các điểm M, O lần lượt là trung điểm của SA và AC

⇒ OM là một đường trung bình tam giác SAC

⇒ OM // SC

⇒ A đúng

Tương tự như vậy, N và O lần lượt là trung điểm của SD và BD

⇒ ON chính là một đường trung bình tam giác SBD

⇒ ON // SB

Bài 4: Hình bình hành ABCD ta vẽ các tia Ax; By, Cz, Dt song song, không nằm trong (ABCD) và cùng hướng với nhau. Mặt phẳng (α) cắt Ax;By, Cz, Dt lần lượt tại các điểm A’, B’,C’, D’. Trong các khẳng định dưới đây, khẳng định nào là đáp án sai?

A. A’B’C’D’ là một hình bình hành

B. (AA’B’B) // (DD’C’C)

C. AA’ = CC’, BB’ = DD'

D. OO’ // AA’

Trong đó tâm hình bình hành ABCD là điểm O, O’ là giao điểm của A’C’ và B’D’.

Giải:

Xét các phương án sau:

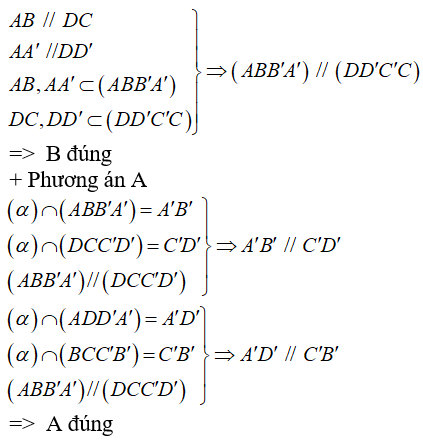
Đáp án D: Do O và O’ lần lượt là trung điểm của AC và A’C’ nên OO’ là đường trung bình trong hình thang AA’C’C. Vậy: OO’ // AA’

⇒ D

Bài 5: Ta có hình vuông ABEF và ABCD nằm ở 2 mặt phẳng khác. Chứng minh (CBE) // (ADF).

Vì ABCD là hình vuông nên BC // AD

ABEF cũng là hình vuông suy ra BE // AF

Xét mặt phẳng (ADF) và (CBE) có:

Đăng ký ngay để được các thầy cô tổng hợp kiến thức và xây dựng lộ trình ôn thi tốt nghiệp THPT đạt 9+ sớm từ bây giờ

Trên đây là toàn bộ kiến thức về chứng minh hai mặt phẳng song song cùng các dạng bài thường gặp kèm lời giải chi tiết cho các bạn học sinh. Mong rằng qua bài viết trên, các em có thể tự tin làm bài và nắm vững kiến thức ôn thi THPT Quốc gia môn Toán. Để học nhiều hơn những kiến thức và bài giảng về toán học lớp 11, truy cập trang web Vuihoc.vn ngay hôm nay nhé!