Công thức tính diện tích hình bình hành, chu vi hình bình hành
Công thức tính diện tích, chu vi hình bình hành là một kiến thức cơ bản, mời các bạn cùng tham khảo công thức mà Quantrimang.com đã tổng hợp sau đây.
1. Diện tích hình bình hành
Diện tích hình bình hành được đo bằng độ lớn của bề mặt hình, là phần mặt phẳng ta có thể nhìn thấy của hình bình hành.
Diện tích hình bình hành được tính theo công thức bằng tích của cạnh đáy nhân với chiều cao.
SABCD = axh
Trong đó:
- S là diện tích hình bình hành.
- a là cạnh đáy của hình bình hành.
- h là chiều cao, nối từ đỉnh tới đáy của một hình bình hành.
2. Chu vi hình bình hành
Chu vi hình bình hành được tính bằng tổng độ dài các đường bao quanh hình, cũng chính là đường bao quanh toàn bộ diện tích, bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.
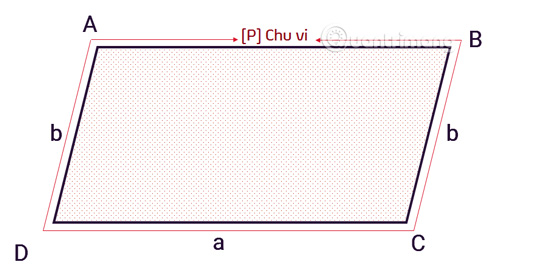
Nói cách khác, chu vi hình bình hành là tổng độ dài của 4 cạnh. Công thức cụ thể như sau:
C = 2 x (a+b)
Trong đó:
- C là chu vi hình bình hành.
- a và b là cặp cạnh kề nhau của hình bình hành.
3. Hình bình hành là hình gì?
Định nghĩa
Hình bình hành là tứ giác có 2 cặp cạnh đối song song hoặc 1 cặp cạnh đối song song và bằng nhau. Hình bình hành có 2 góc đối bằng nhau, 2 đường chéo cắt nhau tại trung điểm của hình.
Có thể coi hình bình hành là 1 trường hợp đặc biệt của hình thang.
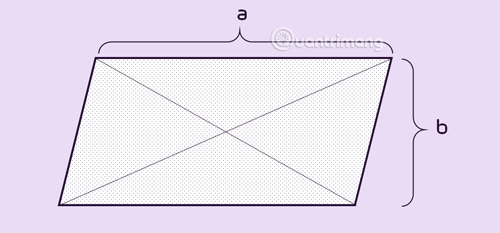
Tính chất hình bình hành
Trong hình bình hành:
- Các cạnh đối bằng nhau.
- Các góc đối bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Dấu hiệu nhận biết
a) Tứ giác có các cạnh đối song song là hình bình hành.
b) Tứ giác có các cạnh đối bằng nhau là hình bình hành.
c) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
d) Tứ giác có các góc đối bằng nhau là hình bình hành.
e) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
4. Câu hỏi trắc nghiệm ôn tập về hình bình hành
Bài 1: Hãy chọn câu sai.
A. Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường
B. Hình bình hành có hai góc đối bằng nhau
C. Hình bình hành có hai đường chéo vuông góc với nhau
D. Hai bình hành có hai cặp cạnh đối song song
Lời giải
Trong hình bình hành:
+ Hình bình hành có các cạnh đối song song
+ Các cạnh đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường nên C sai
Đáp án cần chọn là: C
Bài 2: Cho hình bình hành ABCD có Â = α > 900. Ở phía ngoài hình bình hành vẽ các tam giác đều ADE, ABF. Tam giác CEF là tam giác gì? Chọn câu trả lời đúng nhất
A. Tam giác
B. Tam giác cân
C. Tam giác đều
D. Tam giác tù
Đáp án:
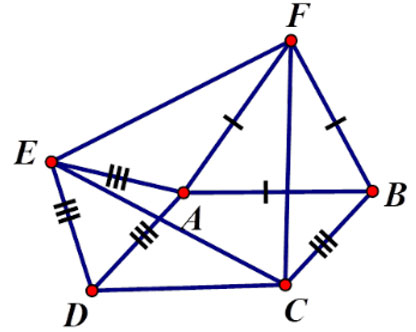
⇒ ΔFBC = ΔFAE (c.g.c) ⇒ CF = FE (2)
Từ (1) và (2) suy ra CF = FE = EC nên tam giác CEF đều
Bài 3: Chọn câu sai. ABCD là hình bình hành. Khi đó:
A. AB = CD
B. AD = BC
C. Trắc nghiệm Hình bình hành có đáp án
D. AC = BD
Lời giải
Trong hình bình hành:
+ Hình bình hành có các cạnh đối song song
+ Các cạnh đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường nên D sai
Bài 4: Điền cụm từ thích hợp vào chỗ trống: “Tứ giác có hai đường chéo … thì tứ giác đó là hình bình hành”.
A. bằng nhau
B. cắt nhau
C. cắt nhau tại trung điểm mỗi đường
D. song song
Lời giải
Dấu hiệu nhận biết:
Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Bài 5: Hãy chọn câu sai:
A. Tứ giác có hai cặp cạnh đối song song là hình bình hành
B. Hình thang có hai góc kề một đáy bằng nhau là hình bình hành
C. Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành
D. Tứ giác có hai cặp góc đối bằng nhau là hình bình hành
Lời giải
Dấu hiệu nhận biết:
+ Tứ giác có các cạnh đối song song là hình bình hành nên A đúng
+ Tứ giác có các cạnh đối bằng nhau là hình bình hành nên D đúng
+ Tứ giác có các góc đối bằng nhau là hình bình hành nên D đúng
Nhận thấy hình thang có hai góc kề một đáy bằng nhau là hình thang cân nên B sai
Đáp án cần chọn là: B
5. Ví dụ về tính chu vi, diện tích hình bình hành
Ví dụ 1: Cho hình bình hành có cạnh đáy bằng 12cm, cạnh bên bằng 7cm, chiều cao bằng 5cm. Hãy tính chu vi và diện tích của hình bình hành đó?
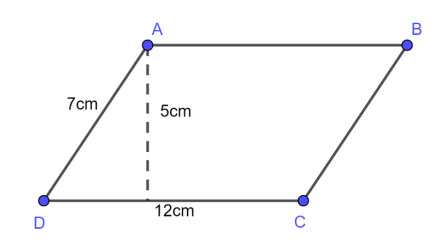
Giải:
Chu vi của hình bình hành là:
P = 2 x (12 + 7) = 38 (cm)
Diện tích hình bình hành là:
S = a x h = 12 x 5 = 60 (cm2)
Ví dụ 2:
Cho hình bình hành ABCD có H, K lần lượt là các chân đường cao kẻ từ đỉnh A,C xuống BD.
a) Chứng minh AHCK là hình bình hành.
b) Gọi O là trung điểm của HK. Chứng minh A, O, C thẳng hàng.
Hướng dẫn:
a) Từ giả thiết ta có:
⇒ AH//CK. ( 1 )
Áp dụng tính chất về cạnh của hình bình hành và tính chất của các góc so le ta có:
⇒ Δ ADH = Δ CBK
(trường hợp cạnh huyền - góc nhọn)
⇒ AH = CK (cạnh tương tứng bằng nhau) ( 2 )
Từ ( 1 ) và ( 2 ) ta có tứ giác AHCK có cặp cạnh đối song song và bằng nhau là hình bình hành.
b) Áp dụng tính chất đường chéo của hình bình hành AHCK
Hình bình hành AHCK có hai đường chéo AC và HK cắt nhau tại trung điểm mỗi đường. Do O là trung điểm của HK nên O cũng là trung điểm của AC
⇒ A, O, C thẳng hàng.
Ngoài hình bình hành, công thức tính diện tích và chu vi của các hình học phổ biến khác như hình thoi, hình vuông, hình thang, hình chữ nhật... cũng rất quan trọng, được áp dụng nhiều trong học tập và cuộc sống.
Hi vọng qua bài viết trên đây, bạn đã hiểu rõ hơn và nắm được những kiến thức cơ bản về hình bình hành. Hãy để lại comment bên dưới nếu bạn có thắc mắc hoặc ý kiến trao đổi với Quantrimang.com nhé.
Link nội dung: https://getairvestal.com/cong-thuc-tinh-dien-tich-hinh-binh-hanh-chu-vi-hinh-binh-hanh-a15652.html