Bí Mật Đằng Sau Công Thức Tính Diện Tích Tứ Giác
Tứ giác, không chỉ là một hình học đơn thuần, mà còn là bức tranh kỳ diệu với 4 góc khác nhau, mỗi góc là một câu chuyện. Cùng khám phá những dạng tứ giác lồi, tứ giác đều, và bài tập thực hành.
Khám Phá Hình Tứ Giác - Khi Công Thức Nâng Cao Kiến Thức
1. Bí Mật Công Thức
Công Thức Hiệu Quả Cho Mọi Loại Tứ Giác
* Diện Tích Tứ Giác Phổ Biến:
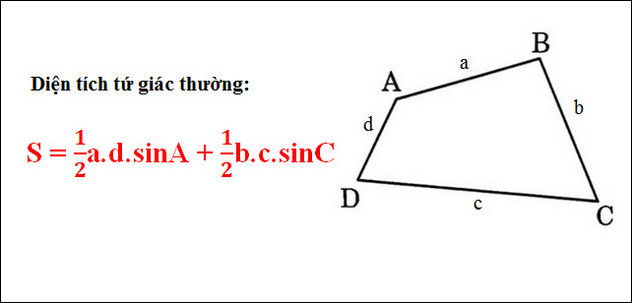
Trong trường hợp này, a, b, c, d đại diện cho chiều dài của những cạnh liên tiếp
* Diện Tích Hình Bình Hành:
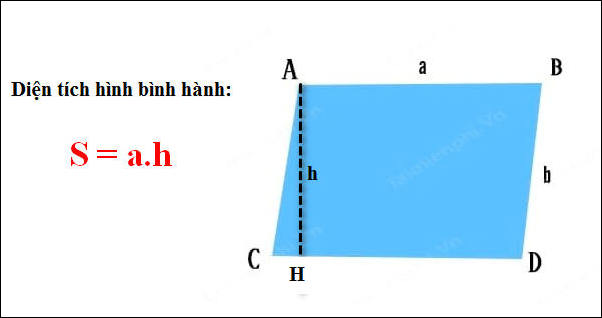
Đơn giản hóa với
- a là chiều dài đáy- h là chiều cao
* Diện Tích Tứ Giác Vuông (Diện Tích Hình Vuông):
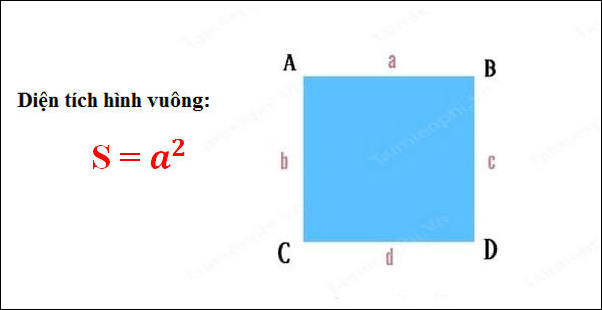
Trong trường hợp này, a là chiều dài của cạnh hình vuông
* Diện Tích Hình Chữ Nhật:
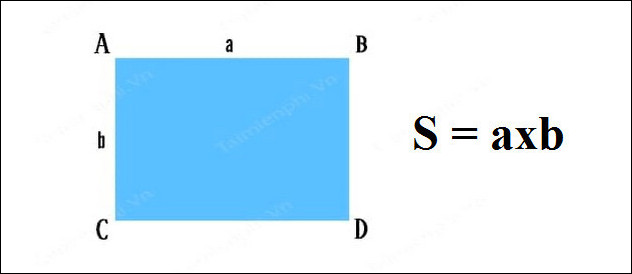
Đơn giản với
- a là chiều dài- b là chiều rộng
* Diện Tích Hình Thoi:
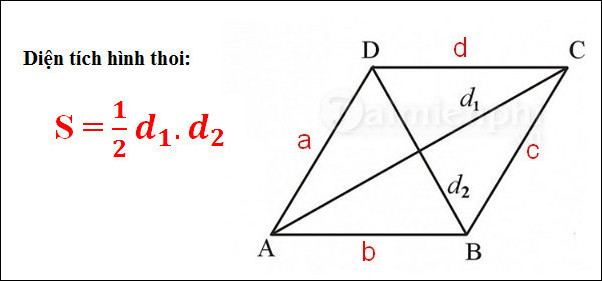
Trong trường hợp này, d1 và d2 lần lượt là độ dài của hai đường chéo của hình thoi
* Diện Tích Hình Thang:
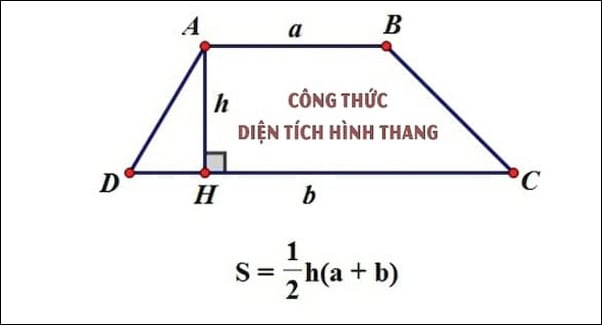
Trong trường hợp này:
- a, b lần lượt là chiều dài và chiều rộng đáy của hình thang- h là đường cao nối từ đỉnh đến đáy của hình thang
Lưu ý: Trong lý thuyết, chúng ta có thể áp dụng các công thức tính diện tích tứ giác ở trên cho mọi tứ giác trong hình học phẳng hoặc không gian Oxyz. Tuy nhiên, cách tính này có thể gây khó khăn cho người học. Do đó, trong hệ tọa độ Oxyz, diện tích tứ giác thường được tính bằng cách sử dụng tích có hướng của hai vectơ. Tuyến sinh viên sẽ học về kiến thức này trong chương trình môn Toán học THPT và không được giới thiệu thêm trong bài viết này.
2. Các Dạng Bài Tính Diện Tích Tứ Giác
* Loại 1 : Tính diện tích của tứ giác đều (thuộc một trong các loại tứ giác đặc biệt như hình bình hành, hình thang, hình thoi,...)
- Áp dụng công thức đã cho, thay các giá trị đã biết và tính toán để hoàn thành bài tập.
* Loại 2 : Khi tứ giác thuộc hình bất kì, không nằm trong các loại đã nêu ở trên và có độ dài các cạnh không bằng nhau, không có cặp cạnh nào song song, áp dụng công thức tính diện tích tứ giác như sau: Giả sử đề bài cung cấp độ dài bốn cạnh của tứ giác là a, b, c, d, trong đó cạnh a đối diện với cạnh c, cạnh b đối diện với cạnh d.
TH1: Trong trường hợp tứ giác nội tiếp, áp dụng công thức tính diện tích tứ giác nội tiếp Brahmagupta:
Trong đó:
Chứng minh cho công thức trên:

- Diện tích tứ giác là S = [(ab + cd)sin B]/2, với B là góc được tạo bởi hai đường chéo của tứ giác
- Diện tích tứ giác cũng có thể tính bằng S = 2R2sinAsinBsin0, với R là bán kính của đường tròn nội tiếp tứ giác
Dạng 2: Áp dụng công thức Bretschneide nếu tứ giác không nội tiếp.
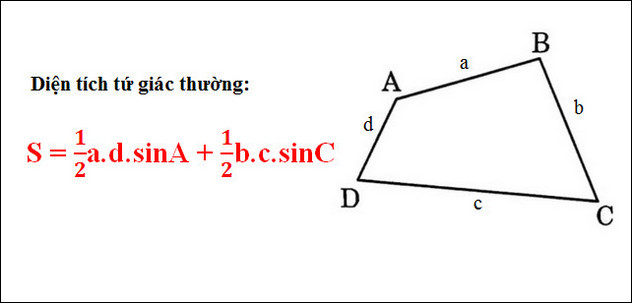
Dạng 3: Tính diện tích hình tứ giác bất kỳ khi biết trước 4 cạnh và hai đường chéo m, n.
Sử dụng công thức: S = [(ab + cd)sin B]/2, với B là góc được tạo bởi hai đường chéo của tứ giác.
3. Bài tập tính diện tích tứ giác
Bài 1: Tính diện tích tứ giác khi biết 4 cạnh
Cho tứ giác ABCD, cạnh AB = 3cm, cạnh BC = 5cm, cạnh CD = 2cm, cạnh DA = 6cm. Góc A = 110 độ, góc C = 80 độ.
Bài giải: S = 0,5.a.d.sinA + 0,5.b.c.sinC=> Diện tích tứ giác ABCD là S = 0,5.3.6.sin110 + 0,5.5.2.sin 80 = 13.371 cm2
Diện tích của tứ giác ABCD là 13,371cm2
Bài 2: Tính diện tích hình thang khi biết đáy AB = 3cm, đỉnh A đến đáy DC là 5cm.
Bài giải: S = (a+b)/2 x h=> Diện tích hình thang là S = (3 + 7)/2 x 5 = 25 cm2
Diện tích hình thang là 25cm2
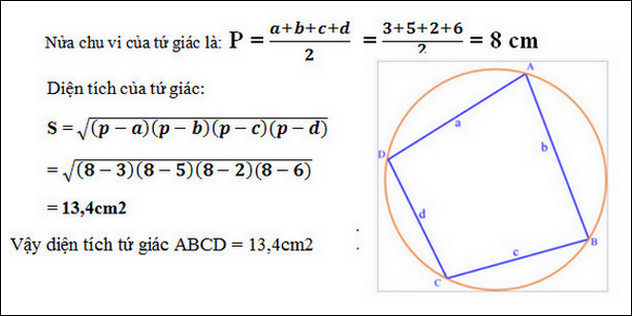
Bài 3: Cho tứ giác nội tiếp ABCD, cạnh AB = 3cm, cạnh BC = 5cm, cạnh CD = 2cm, cạnh DA = 6cm. Tính diện tích tứ giác ABCD.
Bài giải: Cùng tìm hiểu cách tính diện tích hình chữ nhật và áp dụng vào các bài tập.
Với bài viết trên đây, giúp củng cố cách tính diện tích hình chữ nhật và áp dụng vào các bài tập tính toán.
Tham khảo thêm các công thức toán học trên Mytour để nâng cao kiến thức môn Toán và giải các bài tập liên quan.
Để nhớ cách tính diện tích hình thang, có thể tham khảo bài thơ ngắn và thú vị giúp việc học công thức trở nên đơn giản hơn.
Link nội dung: https://getairvestal.com/bi-mat-dang-sau-cong-thuc-tinh-dien-tich-tu-giac-a15682.html