Xác định tâm đường tròn ngoại tiếp

Bài toán xác định tâm của đường tròn ngoại tiếp, đường tròn nội tiếp tam giác cũng như dạng bài tâm đường tròn ngoại tiếp tứ giác là các dạng bài tập trong chương trình toán 9 thường xuyên xuất hiện trong các đề thi. Đặc biệt đây cũng là dạng bài được rất nhiều thầy cô ôn tập cho các em học sinh trong giai đoạn ôn thi vào 10 môn Toán. HOCMAI tổng hợp, biên soạn và giới thiệu tới các em học sinh các dạng cũng như phương pháp để xác định tâm đường tròn ngoại tiếp. Hy vọng với kiến thức của bài viết này sẽ giúp các em có thêm kiến thức và góp phần giúp các em đạt được kết quả cao trong bài thi vào 10 trong thời gian sắp tới.

A. Các cách xác định tâm đường tròn ngoại tiếp

1. Xác định tâm đường tròn ngoại tiếp tam giác

+ Tâm của đường tròn ngoại tiếp tam giác chính là giao điểm của 3 đường trung trực của tam giác đó.

+ Trong trường tam giác vuông, tâm của đường tròn ngoại tiếp chính là trung điểm của cạnh huyền

+ Trong trường hợp tam giác là tam giác đều, tâm của đường tròn ngoại tiếp là giao điểm của 3 đường trung tuyến (do trong trường hợp đường trung tuyến trùng với đường trung trực)

2. Xác định tâm đường tròn nội tiếp của tam giác

+ Tâm của đường tròn nội tiếp của tam giác là giao điểm của ba đường phân giác kẻ từ 3 đỉnh của tam giác đó

3. Xác định tâm của đường tròn ngoại tiếp tứ giác

+ Tứ giác có bốn đỉnh cách đều 1 điểm thì điểm đó chính là tâm của đường tròn ngoại tiếp

+ Quỹ tích của các điểm nhìn về đoạn thẳng AB dưới một góc ᴠuông (90 độ) là một đường tròn có đường kính bằng chiều dài đoạn thẳng AB.

Các em học sinh có thể tham khảo thêm bài viết: Cách chứng minh tứ giác nội tiếp

B. Một số bài tập thực hành xác định tâm đường tròn ngoại tiếp

Bài tập số 1: Hãy xác định tâm và bán kính đường tròn ngoại tiếp của tam giác ABC. Biết rằng tam giác ABC là tam giá đều với các cạnh có kích thước là 6cm.

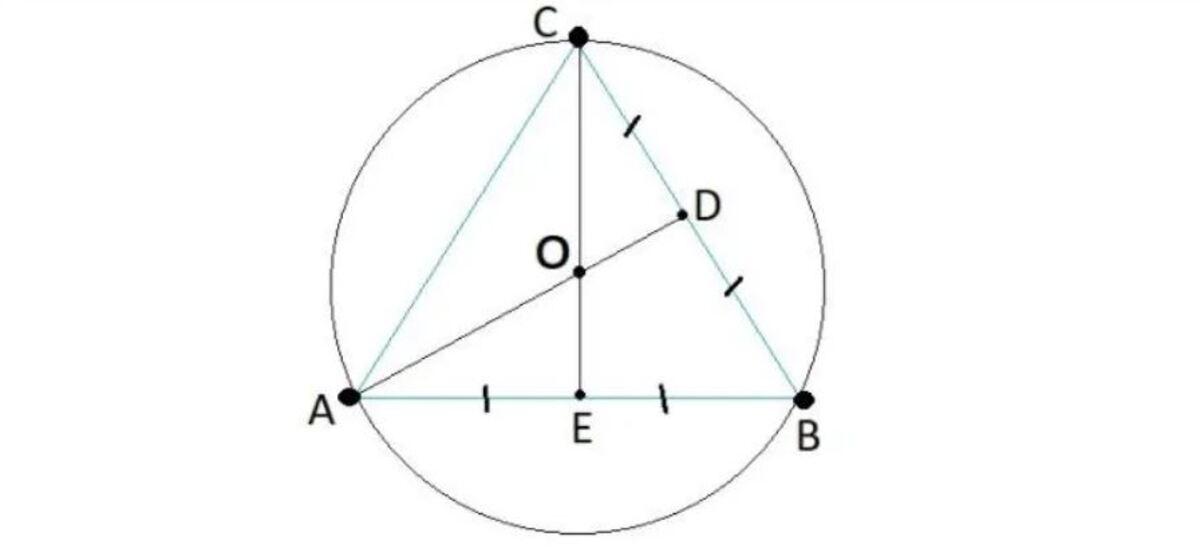
Hướng dẫn giải

Gọi lần lược các điểm D là trung điểm của cạnh BC; điểm E là trung điểm của cạnh AB. Ta gọi giảm điểm của đoạn thẳng AD sẽ giao với cạnh CE là điểm O

Do tam giác ABC đều nên đường trung tuyến đồng thời cũng là đường cao, đường phân giác và đường trung trực của tam giác ABC.

Từ những điều trên, điểm O chính là giao điểm của 3 đường trung trực nên ta có thể suy ra O là tâm của đường tròn ngoại tiếp tam giác.

Tam giác ABC có CE là đường trung tuyến => CE cũng chính là đường cao.

Áp dụng định lý Py ta go trong tam giác vuông AEC ta có:

CE^2 = AC^2 - AE^2 = 36 - 9 = 25 suy ra CE = 5.

Bên cạnh đó ta có điểm O là trọng tâm của tam giác ABC nên suy ra: CO = 2/3 CE = 2/3 x 5 = 10/3.

Như vậy, tâm của đường tròn ngoại tiếp tam giác ABC có trọng tâm O và bán kính là OC = 10/3.

Bài tập số 2: Cho tam giác ABC cân tại A, có đường cao AD, BE và CF cắt nhau tại giao điểm H. Hãy chứng minh tứ giác AEHF là một tứ giác nội tiếp và xác định tâm I của đường tròn ngoại tiếp của tứ giác AEHF đó.

Hướng dẫn giải

Gọi I là trung điểm của cạnh AH. Bên cạnh đó, HF vuông góc với AF (theo đề bài ra) nên suy ra tam giác AFH vuông tại điểm F.

Điểm I là trung điểm của cạnh huyền AH từ đó ta có độ dài IA = IF = IH (1).

Ta có cạnh HE vuông góc với AE (căn cứ theo giả thiết đề bài đã ra).

Từ đó suy ra tam giác AEH là tam giác vuông tại điểm E. Điểm I là trung điểm của cạnh huyền AH.

IA = IF = IH (2)

Từ (1) và (2) suy ra được IA = IF = IH = IE. Vậy điểm I cách đều bốn đỉnh là A, E, H và F. Từ đó ta ta có tứ giác AEHF là tứ giác nội tiếp đường tròn có điểm I là tâm với I là trung điểm của cạnh huyền AH

Bài tập 3: Hãy tìm toạ độ tâm của đường tròn ngoại tiếp của tam giác ABC. Biết rằng các điểm của tam giác ABC lần lượt có tọa độ là A(1;2), B(-1; 0), C(3;2).

Hướng dẫn giải

Ta gọi điểm I có toạ độ là (x; y) là tâm của đường tròn ngoại tiếp tam giác ABC.

C. Một số bài tập tự luyện xác định tâm đường tròn ngoại tiếp

Bài tập số 1

Cho tam giác ABC có 2 đường cao AD và BE cắt nhau tại điểm H và cắt đường tròn O ngoại tiếp tam giác ABC tại các điểm lần lượt tại điểm I và K. Yêu cầu:

Chứng minh rằng tứ giác CDHE nội tiếp đường tròn. Hyax xác định tâm của đường tròn ngoại tiếp tứ giác đó.

Chứng minh rằng tam giác CIK cân.

Bài tập số 2

Cho tam giác ABC có ba góc nhọn nội tiếp với đường tròn O có tâm là điểm R. Theo đó, ba đường của tam giác là AF, BE và CD cắt nhau tại điểm H. Chứng minh rằng tứ giác BDEC nội tiếp đường tròn và hãy xác định tâm của đường tròn ngoại tiếp tứ giác BDCE đó.

Bài tập số 3

Cho một tam giác ABC cân tại điểm A, có 2 cạnh AB = AC nội tiếp đường tròn tâm O. Đồng thời, các đường cao AQ, BE, CF cắt nhau tại một điểm.

Chứng minh tứ giác AEHF là tứ giác nội tiếp đường tròn. Hãy xác định tâm của đường tròn ngoại tiếp đó

Cho bán kính của đường tròn = 2cm, góc BAC = 50 độ. Hãy tính độ dài cung EHF của đường tròn tâm I và diện tích của hình quạt tròn IEHF.

Bài tập số 4

Cho các đường cao AD, BE của tam giác ABC cắt nhau tại giao điểm H (với góc C là góc không vuông) và cắt đường tròn (O) là đường tròn ngoại tiếp tam giác ABC lần lượt tại I và K.

a, Chứng minh rằng tứ giác CDHE là tứ giác nội tiếp và hãy xác định tâm của đường tròn ngoại tiếp tứ giác đó

b, Chứng minh tằng tam giác CIK là tam giác cân

Bài tập số 5

Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O; R). Ba đường của tam giác là AF, BE và CD cắt nhau tại H. Chứng minh tứ giác BDEC là tứ giác nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác

Bài tập số 6

Cho tam giác ABC vuông tại A , có cạnh AB < AC và đường cao AH (điểm H thuộc cạnh huyền BC). Lấy điểm D thỏa mãn điều kiện H là trung điểm của BD. Gọi điểm E là chân đường vuông góc hạ từ điểm C xuống đường thẳng AD. Chứng minh rằng tứ giác AHEC nội tiếp và hãy xác định vị trí tâm O của đường tròn ngoại tiếp tứ giác AHEC.

Bài tập số 7

Cho tam giác ABC nhọn nội tiếp đường tròn (O) (điều kiện đoạn AB < AC). Gọi điểm H là giao điểm của các đường cao AI, BM, CN của tam giác ABC. Đường thẳng BC giao với đường thẳng MN tại D. Hãy chứng minh rằng là tứ giác BNMC nội tiếp. Hãy xác định tâm K của đường tròn trên.

Bài tập số 8

Cho tam giác nhọn ABC nội tiếp đường tròn (O; R). AD, BE, CF lần lượt là các đường cao của tam giác ABC và các đoạn thẳng này cắt nhau tại H.

a, Chứng minh rằng bốn điểm B, F, E, C cùng thuộc một đường tròn

b, Kẻ đường kính AK của đường tròn (O). Tứ giác BHCK là hình gì? Vì sao?

c, Chứng minh H là tâm đường tròn nội tiếp tam giác DEF

Trên đây là toàn bộ kiến thức các em học sinh cần nắm được về xác định tâm đường tròn nội tiếp. Hy vọng rằng với bài viết trên sẽ giúp các em học sinh có thêm kiến thức cần thiết để giải quyết các dạng bài tập liên quan và đạt kết quả cao trong các kì thi sắp tới.