Tiêu chuẩn quốc gia TCVN 7870-2:2010 (ISO 80000-2:2009) về Đại lượng và đơn vị - Phần 2: Dấu và ký hiệu toán học dùng trong khoa học tự nhiên và công nghệ Số hiệu TCVN7870-2:2010 - LawNet
Số mục
Dấu, ký hiệu, biểu thức
Ý nghĩa, diễn đạt bằng lời
Chú thích và ví dụ
2-4.1
(11-3.1)
p Ù q
hội của p và q, p và q
2-4.2
(11-3.2)
p Ú q
tuyển của p và q, p hoặc q
Từ “hoặc” là không bao gồm, nghĩa là p Ú q là đúng, nếu hoặc p hoặc q, hoặc cả hai là đúng.
2-4.3
(11-3.3)
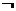p
phủ định của p, không p
2-4.4
(11-3.4)
p Þ q
p kéo theo q, nếu p thì q
q Ü p có cùng nghĩa như p Þ q.
Þ là dấu kéo theo.
2-4.5
(11-3.5)
p Û q
p tương đương với q
(p Þ q) Ù (q Þ p) có cùng nghĩa như p Û q.
Û là dấu tương đương.
2-4.6
(11-3.6)
" x Î A p(x)
với mỗi x thuộc A, mệnh đề p(x) là đúng
Trong trường hợp rõ ràng tập đang xét là tập A thì có thể dùng ký hiệu "x p(x).
" là lượng từ toàn thể. Đối với x Î A, xem 2-5.1.
2-4.7
(11-3.7)
$ x Î /1 p(x)
tồn tại một x thuộc A để p(x) là đúng
Trong trường hợp rõ ràng tập đang xét là tập A thì có thể dùng ký hiệu $ x p(x).
$ là lượng từ bộ phận (tồn tại). Đối với x Î A, xem 2-5.1.
$1x p(x) được dùng để chỉ ra rằng chỉ có đúng một phần tử để p(x) là đúng.
$! cũng được dùng cho $1.
5. Tập hợp
Số mục
Dấu, ký hiệu, biểu thức
Ý nghĩa, diễn đạt bằng lời
Chú thích và ví dụ
2-5.1
(11-4.1)
x Î A
x thuộc A,
...
...
...
A ∍x có cùng nghĩa như x Î A.
2-5.2
(11-4.2)
Y Ï A
y không thuộc A,
y không phải là một phần tử của tập A
A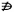
có cùng nghĩa như y Ï A. Gạch phủ định có thể là gạch thẳng.
2-5.3
(11-4.5)
...
...
...
tập các phần tử x1, x2, … , xn
Cũng dùng ký hiệu {xi | i ÎI}, trong đó / là tập các chỉ số.
2-5.4
(11-4.6)
{x Î A | p(x)}
tập các phần tử thuộc A mà ứng với nó mệnh đề p(x) là đúng
VÍ DỤ: {x Î R | x ≤ 5}
Trong trường hợp rõ ràng tập đang xét là tập A thì có thể dùng ký hiệu {x | p(x)} (ví dụ {x |x ≤ 5}, nếu x rõ ràng là biến của các số thực).
2-5.5
...
...
...
card A
|A|
số phần tử trong A, lực lượng của A
Lực lượng có thể là số siêu hạn. Xem thêm 2-9.16.
2-5.6
(11-4.8)
Æ
tập rỗng
...
...
...
(11-4.18)
B Í A
B chứa trong A,
B là một tập con của A
Mọi phần tử của B đều thuộc A. Ì cũng được dùng nhưng xem thêm chú thích cho 2-5.8.
A Ê B có cùng nghĩa như B Í A.
2-5.8
(11-4.19)
B Ì A
...
...
...
B là tập con thực sự của A
Mọi phần tử của B đều thuộc A, nhưng ít nhất một phần tử của A không thuộc B.
Nếu Ì được dùng cho 2-5.7, thì ⊊ phải được dùng cho 2-5.8.
A É B có cùng nghĩa như B Ì A.
2-5.9
(11-4.24)
A È B
hợp của A và B
Tập các phần tử thuộc A hoặc thuộc B hoặc thuộc cả A và B.
...
...
...
2-5.10
(11-4.26)
A Ç B
giao của A và B
Tập các phần tử thuộc cả A và B.
A Ç B = {x | x Î A Ù x Î B}
2-5.11
(11-4.25)
...
...
...
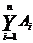
hợp của các tập A1, A2, ..., An
Tập các phần tử thuộc ít nhất một trong các tập A1, A2, ..., An
, 
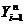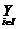và 
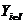cũng được sử dụng trong đó I là tập các chỉ số
2-5.12
(11-4.27)
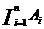
A1 Ç A2 Ç …Ç An
giao của một nhóm các tập A1, …, An
Tập hợp các phần tử thuộc tất cả các tập A1, A2, ..., An
...
...
...
2-5.13
(11-4.28)
A \ B
hiệu giữa A và B, A trừ B
Tập các phần tử thuộc A nhưng không thuộc B.
A \ B= { x | x Î A Ù x Ï B }
Không dùng ký hiệu A - B.
Cũng sử dụng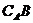 
.
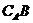chủ yếu được dùng khi B là tập con của A, và có thể bỏ ký hiệu A trong trường hợp rõ ràng tập đang xét là tập A.
2-5.14
...
...
...
(a, b)
cặp có thứ tự a, b,
cặp a, b
(a, b)= (c, d) khi và chỉ khi
a= c và
b= d.
Nếu dấu phẩy có thể hiểu nhầm là dấu thập phân thì có thể sử dụng dấu chấm phẩy (;) hoặc dấu gạch (|)làm dấu phân cách.
2-5.15
(11-4.31)
...
...
...
bộ n phần tử có thứ tự
Xem chú thích cho 2-5.14.
2-5.16
(11-4.32)
A x B
tích đêcac của A và B
Tập các cặp có thứ tự (a, b) sao cho A Î A và B Î B.
A x B= {(x,y)}x Î A Ù y Î B}
2-5.17
...
...
...
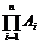
A1 x A2 x …x An
tích đêcac của các tập A1, A2…. An
Tập các bộ n phần tử có thứ tự (x1,x2,…,xn) sao cho x1 Î A1, x2 Î A2, … xn Î An
A x A x... x A được biểu thị bằng An trong đó n số các thừa số trong tích.
2-5.18
(11-4.33)
idA
quan hệ đồng nhất trên A, đường chéo của A x A
...
...
...
trong đó x Î A. Trong trường hợp rõ ràng là tập A thì có thế bỏ chỉ số A.
6. Tập và khoảng số tiêu chuẩn
Số mục
Dấu, ký hiệu, biểu thức
Ý nghĩa, diễn đạt bằng lời
Chú thích và ví dụ
2-6.1 (11.4.9)
N
tập các số tự nhiên,
...
...
...
N= {0.1,2, 3,...}
N*= {1, 2, 3,...}
Các giới hạn khác có thể được thể hiện một cách rõ ràng như trình bày dưới đây.
N>5= {n Î N I n > 5}
Các ký hiệu N và ℕ cũng được sử dụng.
2-6.2 (11.4.10)
Z
tập các số nguyên
Z= {…,-2, -1,0, 1.2,...}
...
...
...
Các giới hạn khác có thể được thể hiện một cách rõ ràng như trình bày dưới đây.
Z³-3= {n Î Z | n ³ -3}
Ký hiệu ℤ cũng được sử dụng.
2-6.3
(11.4.11)
Q
tập các số hữu tỷ
Q*= {r Î Q| r ¹ 0}
Các giới hạn khác có thể được thể hiện một cách rõ ràng như trình bày dưới đây.
...
...
...
Các ký hiệu Q và ℚ cũng được sử dụng.
2-6.4 (11.4.12)
R
tập các số thực
R*= {x Î R | x ¹ 0}
Các giới hạn khác có thể được thể hiện một cách rõ ràng như trình bày dưới đây.
R³0= {x Î R | x ³ 0}
Các ký hiệu R và ℝ cũng được sử dụng.
2-6.5 (11.4.13)
...
...
...
tập các số phức
C*= {z Î C | z ¹ 0}
Các ký hiệu C và ℂ cũng được sử dụng.
2-6.6
(-)
P
tập các số nguyên tố
P= {2, 3, 5, 7,11, 13, 17,...}
Các ký hiệu P và ℙ cũng được sử dụng.
...
...
...
[a, b]
khoảng đóng từ a đến b (bao gồm cả a và b)
[a, b]= {xÎ R | a ≤ x ≤ b}
2-6.8 (11.4.15)
(a, b]
khoảng nửa mở bên trái từ a đến b (không bao a nhưng có bao b)
(a, b]= { x Î R | a < x ≤ b}
Ký hiệu ]a,b] cũng được sử dụng.
2-6.9 (11.4.16)
...
...
...
khoảng nửa mở bên phải từ a đến b (bao a nhưng không bao b)
[a, b)= {x Î R | a ≤ x < b}
Ký hiệu [a, b[ cũng được sử dụng.
2-6.10 (11.4.17)
(a, b)
khoảng mở từ a đến b (không bao gồm cả a và b)
(a, b)= {x Î R | a < x < b}
Ký hiệu ]a, b[ cũng được sử dụng.
2-6.11
...
...
...
(-¥, b]
khoảng đóng không giới hạn đến và bao gồm cả b
(-¥, b]= { x Î R | x ≤ b)
Ký hiệu ]-¥, b] cũng được sử dụng.
2-6.12
(-)
(-¥, b)
khoảng mở không giới hạn đến và không bao gồm b
(-¥, b)= { x Î R | x < b}
...
...
...
2-6.13
(-)
[a,+ ¥)
Khoảng đóng không giới hạn từ a và bao gồm cả a
[a,+ ¥)= (x Î R | a ≤ x}
Ký hiệu [a, ¥[, [a, +¥[ và [a, ¥) cũng được sử dụng.
2-6.14
(-)
(a,+ ¥)
...
...
...
(a,+ ¥)= { x Î R | a < x}
Ký hiệu ]a, +¥,[, ],a ¥[ và (a, ¥) cũng được sử dụng.
7. Dấu và ký hiệu hỗn hợp
Số mục
Dấu, ký hiệu, biểu thức
Ý nghĩa, diễn đạt bằng lời
Chú thích và ví dụ
2-7.1
(11-5.1)
...
...
...
a bằng b
Có thể dùng dấu= để nhấn mạnh rằng đẳng thức cụ thể là đồng nhất thức.
Xem thêm 2-7.18.
2-7.2
(11-5.2)
a ¹ b
a khác b
Gạch phủ định cũng có thể là gạch thẳng.
2-7.3 (11-5.3)
...
...
...
a theo định nghĩa bằng b
VÍ DỤ:
p := mv, trong đó p động lượng, m là khối lượng và v là vận tốc.
Ký hiệu= def và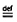 
cũng được sử dụng.
2-7.4
(11-5.4)
a ≙ b
a tương ứng với b
VÍ DỤ:
...
...
...
2-7.5 (11-5.5)
a » b
a xấp xỉ bằng b
Xấp xỉ có đủ tin cậy hay không là tùy thuộc vào người sử dụng. “Bằng” không bao gồm trong phép xấp xỉ.
2-7.6
(11-7.7)
a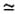
b
a tiệm cận với b
VÍ DỤ:
...
...
...
(Về x ® a, xem 2-7.16)
2-7.7 (11-5.6)
a ~ b
a tỷ lệ với b
Dấu ~ cũng được dùng đối với quan hệ tương đương.
Ký hiệua ∝bcũng được sử dụng.
2-7.8
(-)
M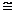
N
...
...
...
M đẳng cấu với N
M là N các tập điểm (số liệu hình học).
Dấu này cũng được dùng cho phép đẳng cấu của cấu trúc toán học.
2-7.9
(11-5.7)
a < b
a nhỏ hơn b
2-7.10
...
...
...
B > a
b lớn hơn a
2-7.11 (11-5.9)
a ≤ b
a nhỏ hơn hoặc bằng b
2-7.12 (11-5.10)
b ³ a
...
...
...
2-7.13 (11-5.11)
a ≪ b
a rất nhỏ so với b
a có đủ nhỏ so với b hay không là tùy thuộc vào người sử dụng.
2-7.14 (11-5.12)
b ≫ a
b rất lớn so với a
b có đủ lớn so với a hay không là tùy thuộc vào người sử dụng.
...
...
...
(11-5.13)
¥
vô hạn
Ký hiệu này không thể hiện một số nhưng thường là bộ phận của nhiều biểu thức liên quan đến các giới hạn.
Các ký hiệu +¥, -¥ cũng được sử dụng.
2-7.16 (11-7.5)
x ® a
x tiến tới a
Ký hiệu này xuất hiện như một bộ phận của nhiều biểu thức liên quan đến các giới hạn.
...
...
...
2-7.17 (-)
m | n
m chia n
Đối với các số nguyên m và n:
$ k Î z m×k= n
2-7.18
(-)
n º k mod m
n là đồng dư với k mod m
...
...
...
Xem thêm 2-7.1.
2-7.19
(1-5.14)
(a + b)
[a + b]
{a + b}
<a + b>
dấu ngoặc đơn dấu ngoặc vuông dấu móc dấu ngoặc nhọn
Chỉ nên sử dụng dấu ngoặc đơn để nhóm, vì các dấu ngoặc và dấu móc có nghĩa riêng trong các lĩnh vực cụ thể. Dấu ngoặc đơn có thể lồng vào nhau mà vẫn không bị lẫn.
...
...
...
Số mục
Dấu, ký hiệu, biểu thức
Ý nghĩa, diễn đạt bằng lời
Chú thích và ví dụ
2-8.1
(11-5.15)
AB || CD
đường thẳng AB song song với đường thẳng CD
Viết g || h nếu g và h là hai đường thẳng xác định bởi các điểm A và B, điểm c và D, tương ứng. AB//CD cũng được dùng.
...
...
...
(11-5.16)
AB^CD
đường thẳng AB vuông góc với đường thẳng CD
Viết g ^ h nếu g và h là hai đường thẳng xác định bởi các điểmAvà B, điểm C và D, tương ứng. Trong mặt phẳng, hai đường thẳng này phải cắt nhau.
2-8.3
(-)
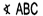
góc ở đỉnh B trong tam giác ABC
Góc này không định hướng, thỏa mãn điều kiện
...
...
...
2-8.4
(-)
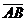
đoạn thẳng từ A đến B
Đoạn thẳng này là tập các điểm giữa A và B trên đường thẳng AB.
2-8.5
(-)
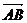
véctơ từ A đến B
...
...
...
2-8.6
(-)
d(A, B)
khoảng cách giữa điểmAvà điểm B
Khoảng cách này là độ dài của đoạn thẳng AB và cũng là độ lớn của véctơ AB.
9. Các phép toán
Số mục
Dấu, ký hiệu, biểu thức
Ý nghĩa, diễn đạt bằng lời
...
...
...
2-9.1
(11-6.1)
a + b
a cộng b
Phép toán này là phép cộng. Dấu + là dấu cộng.
2-9.2 (11-6.2)
a - b
a trừ b
Phép toán này là phép trừ. Dấu - là dấu trừ.
...
...
...
A ± b
a cộng hoặc trừ b
Đây là sự kết hợp hai giá trị trong một biểu thức.
2-9.4 (11-6.4)
a ∓ b
a trừ hoặc cộng b
-(a ±b)= -a ∓ b
2-9.5 (11-6.5)
a •b
...
...
...
a b
ab
a nhân b,alần b
Phép toán này là phép nhân. Ký hiệu dùng cho phép nhân là dấu chấm giữa dòng (•) hoặc dấu nhân (x).
Có thể bỏ các dấu này nếu không có khả năng hiểu nhầm.
Xem thêm 2-5.16, 2-5.17, 2-17.10, 2-17.11, 2-17.22 và 2-17.23 đối với việc sử dụng dấu chấm và dấu nhân trong các tích số khác nhau.
2-9.6 (11-6.6)
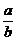
a/b
...
...
...
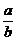= a• b-1
Xem thêm TCVN 7870-1 (ISO 80000-1), 7.1.3.
Đối với tỷ số, dấu: cũng được sử dụng,
VÍ DỤ: Tỷ số giữa độ cao h và chiều rộngbcủa khổ giấy A4 là h: b=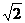 
.
Không nên sử dụng dấu ÷
2-9.7
(11-6.7)
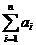
a1 + a2 +...+ an tổng của a1, a2, …, an
...
...
...
Cũng được sử dụng.
2-9.8
(11-6.8)
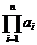
a1 × a2 ×... an, tích của a1, a2, …,an
Ký hiệu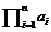 
, 
, 
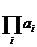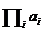và 
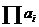
cũng được sử dụng.
2-9.9
(11-6.9)
...
...
...
a lũy thừa p
Diễn đạt bằng lời của a2 làabình phương; diễn đạt bằng lời a3 làalập phương.
2-9.10 (11-6.10)
a1/2
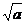
a mũ 1/2, căn bậc hai của a
Nếu a ≥ 0, thì 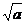³ 0
Nên tránh sử dụng ký hiệu Öa. Xem chú thích của 2-9.11.
2-9.11
...
...
...
a1/n
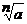
a mũ 1/n, căn bậc n của a
Nếua³ 0, thì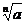 
³ 0.
Nên tránh sử dụng ký hiệu nÖa.
Nếu dùng ký hiệu nÖ hoặc Ö cho một biểu thức tổng hợp thì phải dùng dấu ngoặc đơn để tránh nhầm lẫn.
2-9.12
(11-6.14)
...
...
...
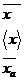
Giá trị trung bình thu được bằng các phương pháp khác là
- trung bình điều hòa biểu thị bằng chỉ số h,
- trung bình hình học biểu thị bằng chỉ số g.
- trung bình toàn phương, biểu thị bằng chỉ số q hoặc rms.
Chỉ có thể bỏ chỉ số trong trường hợp trung bình số học.
Trong toán học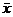 
còn được dùng cho liên hợp phức của x; xem 2-14.6.
2-9.13
(11-6.13)
sgn a
...
...
...
Với số thực a:
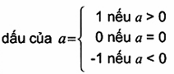
Xem thêm mục 2-14.7.
2-9.14
(-)
inf M
cận dưới của M
Giới hạn dưới lớn nhất của tập không rỗng các số bị chặn từ bên dưới.
2-9.15
...
...
...
sup M
cận trên của M
Giới hạn trên nhỏ nhất của một tập không rỗng các số bị chặn từ phía trên.
2-9.16
(11-6.12)
|a|
giá trị tuyệt đối của a,
mô đun của a,
độ lớn của a
...
...
...
Giá trị tuyệt đối của số thực a.
Mô đun của số phức a; xem 2-14.4.
Độ lớn của véctơ a; xem 2-17.4.
Xem thêm 2-5.5.
2-9.17
(11-6.17)
ëaû
sàn a,
số nguyên lớn nhất nhỏ hơn hoặc bằng số thực a
...
...
...
VÍ DỤ:
ë2,4û= 2
ë-2,4û= -3
2-9.18
(-)
éaù
trần a,
số nguyên nhỏ nhất lớn hơn hoặc bằng số thực a
VÍ DỤ:
...
...
...
é-2,4ù= -2
2-9.19
(-)
int a
phần nguyên của số thực a
int a= sgn a × ë|a|û
VÍ DỤ:
int(2,4)= 2
int(-2,4)= -2
...
...
...
(-)
frac a
phần thập phân của số thực a
frac a=a- inta
VÍ DỤ:
frac(2,4)= 0,4
frac(-2,4)= -0,4
2-9.21
(-)
...
...
...
giá trị nhỏ nhất củaavà b
Phép toán tổng quát hóa cho nhiều số và các tập số. Tuy nhiên, một tập vô hạn các số không nhất thiết có phần tử nhỏ nhất.
2-9.22
(-)
max(a, b)
giá trị lớn nhất của avà b
Phép toán tổng quát hóa cho nhiều số và các tập số. Tuy nhiên, một tập vô hạn các số không nhất thiết có phần tử lớn nhất.
10. Tổ hợp
Trong điều này, n và k là các số tự nhiên, với k ≤ n.
...
...
...
Dấu, ký hiệu, biểu thức
Ý nghĩa, diễn đạt bằng lời
Chú thích và ví dụ
2-10.1 (11-6.15)
n!
giai thừa
n!=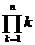 
= 1 × 2 × 3... × n (n > 0)
0!= 1
2-10.2
...
...
...
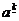
[a]k
giai thừa giảm
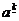=a × ( a- 1)-...-(a - k + 1) (k > 0)
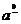= 1
a có thể là số phức.
Đối với số tự nhiên n: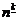 
= 
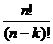
2-10.3
(-)
...
...
...
(a)k
giai thừa tăng
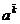=a × ( a+ 1)-...-(a + k - 1) (k > 0)
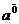= 1
a có thể là số phức.
Đối với số tự nhiên n: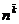 
= 
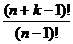
(a)k được gọi là ký hiệu Pochhammer trong lý thuyết về hàm đặc biệt. Tuy nhiên, trong tổ hợp và thống kê, thường sử dụng cùng ký hiệu với giai thừa giảm.
2-10.4
(11-6.16)
...
...
...
hệ số nhị thức
= 
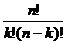(0 ≤ k ≤ n)
2-10.5
(-)
Bn
Số Bernoulli
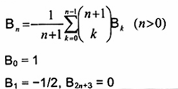
2-10.6
(11-6.16)
...
...
...
Tổ hợp không lặp
= =
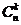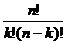
2-10.7
(-)
R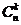
tổ hợp lặp
R =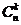 
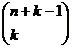
2-10.8
(-)
...
...
...
chuyển vị không lặp
= =
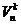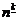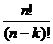
Thuật ngữ “hoán vị” được dùng khi n= k.
2-10.9
(-)
R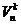
chuyển vị lặp
R 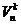= nk
11. Hàm số
...
...
...
Dấu, ký hiệu, biểu thức
Ý nghĩa, diễn đạt bằng lời
Chú thích và ví dụ
2-11.1 (11-7.1)
f, g, h,...
hàm số
Một hàm số ấn định cho đối số bất kỳ trong miền xác định của hàm đó một giá trị duy nhất thuộc miền giá trị.
2-11.2
(11-7.2)
...
...
...
f(x1, …,xn)
giá trị của hàm số f đối với đối số x hoặc đối số (x1),.... xn) tương ứng
Một hàm số có miền xác định là tập các bộ n số là hàm n biến.
2-11.3
(-)
f: A →B
f ánh xạAvào B
Hàm f có miền xác địnhAvà nhận giá trị 5.
2-11.4
...
...
...
f: x 
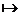T(x)
x Î A
f là hàm số ánh xạ mọi
x Î A thành T(x)
T (x) là biểu thức xác định chỉ ra giá trị của hàm f với đối số x. Vì f (x)= T(x), biểu thức xác định thường được dùng như ký hiệu cho hàm f.
VÍ DỤ: f: x 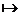3x2y, x Î [0;2]
f là hàm số (phụ thuộc vào tham số y) xác định trong khoảng quy định bởi biểu thức 3x2y.
2-11.5
(-)
...
...
...
f(x)= y.
f ánh xạ x lên y
Ví DỤ: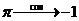 
2-11.6
(11-7.3)
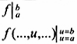
f(b)- f(a)
f(…,b,…) - f(…,a,…)
Ký hiệu này chủ yếu được dùng khi tính tích phân xác định.
...
...
...
g o f
hàm hợp của f và g,
g hợp f
(g o f)(x)= g(f(x))
Trong tổ hợp g ° f, hàm g được áp dụng sau hàm f.
2-11.8 (11-7.6)
Lim f (x)
x → a
limx®a f(x)
...
...
...
f (x) ®bkhi x ®a
có thể viết limx®a f(x)= b.
Giới hạn “từ bên phải” (x > a) và “từ bên trái” (x < a) được biểu diễn tương ứng bằng limx®a +f(x) và limx®a - f(x).
2-11.9
(11-7.8)
f(x)= O(g(x))
f (x) là O lớn của g(x), |f(x)/g(x)| bị chặn từ phía trên trong giới hạn hàm ý theo ngữ cảnh,
f(x) có cùng bậc hoặc bậc thấp hơn so với g(x)
Dấu “ = ” được dùng ở đây vì lý do lịch sử và không có nghĩa bằng do không áp dụng chuyển đổi.
...
...
...
sin x= O (x), khi x ® 0
2-11.10 (11-7.9)
f(x)= o(g(x))
f(x) là o nhỏ g(x),
f(x)/g(x) ® 0 trong giới hạn hàm ý theo ngữ cảnh,
f(x) có bậc cao hơn bậc của g(x)
Dấu “= ” được dùng ở đây vì lý do lịch sử và không có nghĩa bằng do không áp dụng chuyển đổi.
VÍ DỤ:
cos x= 1 + o (x), khi x ® 0
...
...
...
(11-7.10)
Df
deltaf,
số gia hữu hạn của f
Hiệu giữa hai giá trị hàm số hàm ý theo ngữ cảnh.
VÍ DỤ: Dx=x2-x1
Df= f(x2) -f (x1)
2-11.12
(11-7.11)
...
...
...
đạo hàm của hàm số f theo x
Chỉ dùng cho các hàm số một biến.
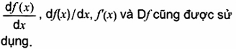
Nếu biến độc lập là thời gian t, thì f& cũng được dùng cho f.
2-11.13 (11-7.12)
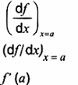
giá trị của đạo hàm của hàm f tại x= a
2-11.14 (11-7.13)
...
...
...
đạo hàm bậc n của hàm f theo x
Chỉ dùng cho các hàm số một biến
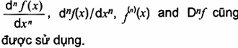
f’’ và f’’’ cũng được dùng tương ứng cho f(2) và f(3).
Nếu biến độc lập là thời gian t, thì f&& cũng được dùng cho f.
2-11.15
(11-7.14)
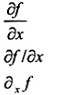
đạo hàm riêng của hàm f theo x
...
...
...
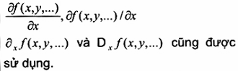Các biến độc lập còn lại có thể được chỉ ra bằng chỉ số dưới, ví dụ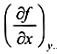 
Ký hiệu đạo hàm riêng này được mở rộng cho các đạo hàm bậc cao hơn, ví dụ:
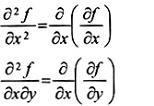
Các ký hiệu khác, ví dụ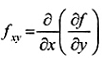 
cũng được sử dụng
2-11.16 (11-7.15)
df
vi phân toàn phần của hàm f
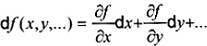
2-11.17
...
...
...
df
biến phân vô cùng bé của hàm f
2-11.18 (11-7.17)
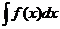
tích phân bất định của hàm f
2-11.19
(11-7.18)
...
...
...
tích phân xác định của hàm f từ A đến b
Đây là trường hợp đơn giản của hàm số xác định trong một khoảng. Cũng có thể tính tích phân của các hàm số xác định trong các lĩnh vực chung hơn. Các ký hiệu đặc biệt, ví dụ: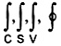 
được dùng cho tích phân đường cong c, mặt s, miền ba chiều V và đường cong khép kín hoặc mặt kín, tương ứng.
Đa tích phân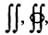 
,... cũng được sử dụng.
2-11.20
(-)
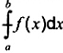
Giá trị chính Cauchy của tích phân của f với f kỳ dị tại c
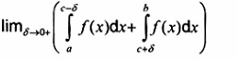
Trong đóa< c < b
...
...
...
(-)
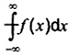
Giá trị chính Cauchy của tích phân của f
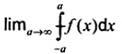
12.Hàm mũ và hàm loga
Có thể sử dụng biến số phức, đặc biệt là đối với cơ số e.
Số mục
Dấu, ký hiệu, biểu thức
Ý nghĩa, diễn đạt bằng lời
...
...
...
2-12.1 (11-8.2)
e
cơ số của loga tự nhiên
e := lim n®¥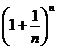 
= 2,718 281 8...
2-12.2
(11-8.1)
ax
a mũ x,
hàm mũ theo cơ sốacủa x
...
...
...
2-12.3
(11-8.3)
ex
exp x
e mũ x,
hàm mũ theo cơ số e của x
Xem 2-14.5.
2-12.4 (11-8.4)
logax
...
...
...
log x được dùng khi không cần thiết phải ghi rõ cơ số.
2-12.5 (11-8.5)
In x
loga tự nhiên của x
In x= loge x
log x không được dùng thay cho In x, Ig x, lb x hoặc logex, log10 x, log2 x
2-12.6
(11-8.6)
Lgx
...
...
...
lgx= log10x
Xem chú thích của 2-12.5.
2-12.7 (11-8.7)
Ib x
loga nhị phân của X
Ibx= log2x
Xem chú thích của 2-12.5.
13 Hàm số vòng và hàm hypecbol
Số mục
...
...
...
Ý nghĩa, diễn đạt bằng lời
Chú thích và ví dụ
2-13.1 (11-9.1)
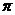
tỷ số giữa chu vi hình tròn và đường kính của nó
p = 3,141 592 6...
2-13.2 (11-9.2)
sin x
sin của x
...
...
...
thường được viết là sinn x, cosn x,...
2-13.3 (11-9.3)
cos x
cosin của x
cos X= sin(x + p/2)
2-13.4 (11-9.4)
tan x
tang của x
tan x= sin x/cos x
...
...
...
2-13.5
(11-9.5)
cot x
cotang của x
cot x= 1/tan x
không nên dùng ctg x.
2-13.6 (11-9.6)
sec x
sec của x
...
...
...
2-13.7
(11-9.7)
csc x
cosec của x
csc x= 1/sin x
cosec x cũng được dùng.
2-13.8
(11-9.8)
arcsin X
...
...
...
y= arcsin x Û x= sin y,
-p /2 ≤ y ≤ p /2
Hàm arcsin là hàm ngược của hàm sin với miền giới hạn như trên.
2-13.9 (11-9.9)
arccos x
arc cosin của x
y= arccos x Û x = cos y, 0 ≤ y ≤ p
Hàm arccos là hàm ngược của hàm cos với miền giới hạn như trên.
2-13.10
...
...
...
arctan x
arc tang của x
y= arctan x Û x = tan y,
-p/2 < y < p/2
Hàm arctan là hàm ngược của hàm tan với miền giới hạn như trên.
Không nên sử dụng arctg x.
2-13.11 (11-9.11)
arccot x
arc cotang của x
...
...
...
Hàm arccot là hàm ngược của hàm cot với miền giới hạn như trên.
Không nên sử dụng arcctg x.
2-13.12 (11-9.12)
arcsec x
arc sec của x
y= arcsec x Û x = sec y,
0 ≤ y ≤ p, y ≠ p/2
Hàm arcsec là hàm ngược của hàm sec với miền giới hạn như trên.
2-13.13 (11-9.13)
...
...
...
arc cosec của x
y= arccsc x Û x = csc y,
(-p/2 ≤ y ≤ p/2, y ≠ 0)
Hàm arccsc là hàm ngược của hàm csc với miền giới hạn như trên.
Nên tránh sử dụng arccosec x.
2-13.14 (11-9.14)
sinh x
sin hypecbol của X
...
...
...
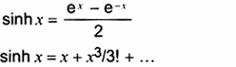
2-13.15
(11-9.15)
cosh x
cosin hypecbol của x
cosh2 x= sinh2 x + 1
Nên tránh sử dụng ch x.
2-13.16 (11-9.16)
tanh x
tang hypecbol của x
...
...
...
Nên tránh sử dụng th x.
2-13.17 (11-9.17)
coth x
cotang hypecbol của x
coth x= 1/tanh x
2-13.18
(11-9.18)
sech x
sec hypecbolcủa x
...
...
...
2-13.19 (11-9.19)
csch x
cosec hypecbol của x
csch x= 1/sinh x
Nên tránh sử dụng cosech x.
2-13.20
(11-9.20)
arsinh x
hàm ngược của sin hypecbol của x, miền sin hypecbol của x
...
...
...
Hàm arsinh là hàm ngược của hàm sinh.
Nên tránh sử dụng arsh x.
2-13.21 (11-9.21)
arcosh x
hàm ngược cosin hypecbol của x, miền cosin hypecbol của x
y= arcosh x Û x = cosh y, y ³ 0
Hàm arcosh là hàm ngược của hàm cosh với miền giới hạn như trên.
Nên tránh sử dụng arch x.
2-13.22
...
...
...
artanh x
hàm ngược tang hypecbol của x, miền tang hypecbol của x
y= artanh x Û x = tanh y
Hàm artanh là hàm ngược của hàm tanh.
Nên tránh sử dụng arth X.
2-13.23
(11-9.23)
arcoth x
hàm ngược cotang hypecbol của x, miền cotang hypecbolcủa x
...
...
...
Hàm arcoth là hàm ngược của hàm coth với miền giới hạn như trên.
2-13.24
(11-9.24)
arsech x
hàm ngược sec hypecbol của x, diện tích sec hypecbolcủa x
y= arsech x Û x = sech y, y ³ 0
Hàm arcech là hàm ngược của hàm sech với miền giới hạn như trên.
2-13.25
(11-9.25)
...
...
...
hàm ngược cosec hypecbol của X, miền cosec hypecbol của X
y= arcsch x Û x = csch y, y ³ 0
Hàm arcsch là hàm ngược của hàm csch Nên tránh sử dụng arcosech X.
14. Số phức
Số mục
Dấu, ký hiệu, biểu thức
Ý nghĩa, diễn đạt bằng lời
Chú thích và ví dụ
2-14.1 (11-10.1)
...
...
...
j
đơn vị ảo
i2= j2= -1
i được dùng trong toán học và vật lý, j được dùng trong kỹ thuật điện.
2-14.2
(11-10.2)
Re z
phần thực của z
z= x + i y
...
...
...
x= Re z và y = lm z.
2-14.3
(11-10.3)
Im z
phần ảo của z
Xem 2-14.2.
2-14.4
(11-10.4)
|z|
...
...
...
|z| =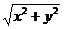 
trong đó x = Re z và y= Im z.
Xem thêm 2-9.16.
2-14.5 (11-10.5)
arg z
góc cực của z
z= r eij
trong đó
r= |z| và j = arg z, -p < j <p nghĩa là Re z= r cos j và
...
...
...
2-14.6 (11-10.6)
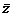
z*
liên hợp phức của z
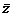chủ yếu dùng trong toán học,
z* chủ yếu dùng trong vật lý và kỹ thuật.
2-14.7
(11-10.7)
sgn z
...
...
...
sgn z = z / |z|= exp(i arg z) (z ≠ 0)
sgn z= 0 đối với z= 0
Xem thêm mục 2-9.13.
15. Ma trận
Ma trận thường được viết bằng chữ hoa đậm, nghiêng, còn các phần tử của ma trận được viết bằng chữ thường nghiêng, tuy nhiên, các dạng chữ khác cũng được sử dụng.
Số mục
Dấu, ký hiệu, biểu thức
Ý nghĩa, diễn đạt bằng lời
Chú thích và ví dụ
...
...
...
(11-11.1)
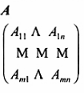
Ma trậnAkiểu m nhân n
A là ma trận với các phần tử aij = (A)ij
m là số hàng và n là số cột.
A= (aij) cũng được sử dụng.
Dấu ngoặc vuông cũng được dùng thay cho dấu ngoặc đơn.
2-15.2
(-)
...
...
...
tổng của ma trậnAvà B
(A + B)ij= (A)ij + (B)ij
Ma trậnAvàBphải có cùng số hàng và số cột.
2-15.3
(-)
x A
tích của đại lượng vô hướng x và ma trận A
(x A)ij= x (A)ij
2-15.4
...
...
...
AB
tích của ma trậnAvà B
Số cột củaAphải bằng số hàng của B.
2-15.5
(11-11.3)
E
i
ma trận đơn vị
...
...
...
Xem 2-17.9.
2-15.6
(11-11.4)
A-1
ma trận nghịch đảo của ma trận vuông A
AA-1= A-1 A= E
2-15.7
(11-11.5)
AT
...
...
...
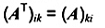
2-15.8
(11-11.6)
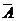
A*
ma trận liên hợp phức của A
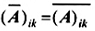
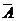được dùng trong toán học,A* được dùng trong vật lý và kỹ thuật điện.
2-15.9
...
...
...
AH
ma trận liên hợp Hermite của A
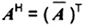
Thuật ngữ “ma trận tiếp giáp” cũng được sử dụng.
A* và A+ cũng được dùng cho AH.
2-15.10
(11-11.8)
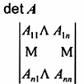
định thức của ma trận vuông A
...
...
...
2-15.11
(-)
rank A
hạng của ma trận A
Hạng của ma trậnAlà số hàng độc lập tuyến tính của A. Nó cũng bằng số cột độc lập tuyến tính của A.
2-15.12
(11-11.9)
tr A
vết của ma trận vuông A
...
...
...
2-15.13
(11-11.10)
||A||
chuẩn của ma trận A
Chuẩn của ma trậnAlà số đặc trưng cho ma trận này và thỏa mãn bất đẳng thức tam giác:
nếuA+ B= C, thì
||A|| + ||B|| ³ ||C||.
Các chuẩn ma trận khác nhau cũng được sử dụng.
...
...
...
Số mục
Các tọa độ
Vị trí vectơ và vi phân của nó
Tên của hệ tọa độ
Chú thích
2-16.1
(11-12.1)
x, y, z
...
...
...
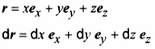
x1, x2, x3 đối với tọa độ và e1, e2, e3 đối với vectơ cơ sở cũng được sử dụng. Ký hiệu này dễ tổng quát cho không gian n chiều.
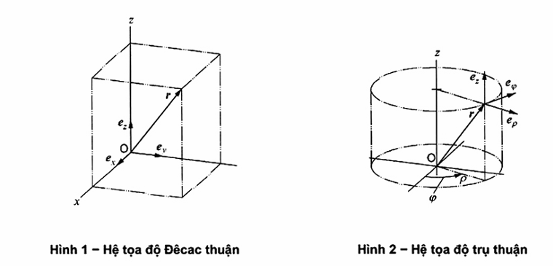
ex, ey, ez , tạo thành một hệ trực chuẩn thuận. Xem các Hình 1 và 4.
Đối với vectơ cơ sở, i, j, k cũng được sử dụng.
2-16.2 (11-12.2)
p,j,z
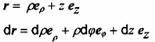
tọa độ trục
ep(j), ej (j), ez tạo thành một hệ trực chuẩn thuận. Xem Hình 2. Nếu 2= 0, thì p và j là các tọa độ cực.
2-16.3
...
...
...
r, J,j
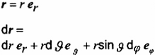
tọa độ cầu
er( J, j), eJ(J, j), ej (j) tạo thành một hệ trực chuẩn thuận. Xem Hình 3.
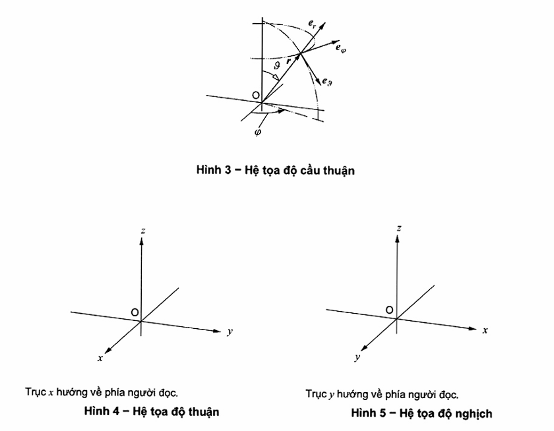
CHÚ THÍCH: Nếu, trường hợp ngoại lệ, sử dụng hệ nghịch (xem Hình 5) thay cho hệ thuận (xem Hình 4) vì mục đích nhất định, thì phải nêu rõ để tránh sai dấu.
17. Đại lượng vô hướng, vectơ và tenxơ
Các đại lượng vô hướng, vectơ và tenxơ là các đối tượng toán học có thể dùng để biểu thị các đại lượng vật lý nhất định và giá trị của chúng. Chúng không phụ thuộc vào lựa chọn cụ thể của hệ tọa độ, trong khi mỗi thành phần của một vectơ hoặc tenxơ và từng vectơ thành phần và tenxơ thành phần lại phụ thuộc vào lựa chọn đó.
...
...
...
Các thành phần Đêcac của vectơ vị trí bằng các thành phần Đêcac của điểm cho bởi vectơ đó.
Thay cho việc coi từng thành phần như một giá trị đại lượng vật lý (nghĩa là một trị số nhân với một đơn vị) thì có thể viết vectơ như một vectơ trị số nhân với một đơn vị. Tất cả các đơn vị đều là vô hướng.
VÍ DỤ:
F= (3 N, -2 N, 5 N)= (3, -2, 5) N (trong tọa độ Đêcac)
trong đó:
F là lực;
3 N là thành phần đầu tiên, ví dụ Fx, của vectơ F có trị số là 3 và đơn vị N (các thành phần còn lại là 2N và 5 N);
(3, -2, 5) là vectơ trị số và N là đơn vị.
Áp dụng xem xét tương tự với tenxơ bậc hai và bậc cao hơn.
...
...
...
nếu chỉ số xuất hiện hai lần trong một số hạng thì tổng được lấy trên miền biến thiên của chỉ số như đã biết, và có thể bỏ ký hiệu S.
Vô hướng là tenxơ bậc không và vectơ là tenxơ bậc một.
Vectơ và tenxơ thường được biểu diễn bằng các ký hiệu chung cho các thành phần của chúng, ví dụ ai cho vectơ, Tij cho tenxơ bậc hai và aibj cho tích nhị thức.
Chữ viết tắt “cycl” có nghĩa là hoán vị vòng quanh của các thành phần và chỉ số. Thay cho việc viết ba công thức thành phần tương tự nhau thì chỉ cần viết một công thức là đủ, hai công thức còn lại tiếp sau bằng cycl, cycl.
Số mục
Dấu, ký hiệu, biểu thức
Ý nghĩa, diễn đạt bằng lời
Chú thích và ví dụ
2-17.1 (11-13.1)
...
...
...
vectơ a
Có thể sử dụng ký hiệu chữ có mũi tên trên đầu thay cho kiểu chữ đậm để chỉ thị vectơ.
2-17.2
(-)
a + b
tổng của vectơavà b
(a + b)i= ai + bi
2-17.3
(-)
...
...
...
tích của một số, lượng vô hướng hoặc thành phần X với vectơ a
(xa)i= xai
2-17.4 (11-13.2)
|a|
a
độ lớn của vectơ a, chuẩn của vectơ a
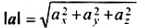
||a|| cũng được dùng. Xem thêm 2-9.16.
2-17.5
...
...
...
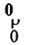
vectơ không
Vectơ không có độ lớn bằng 0.
2-17.6
(11-13.3)
ea
vectơ đơn vị theo phương của a
ea=a|a|,a≠ 0
a= |a|ea
...
...
...
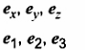
vectơ đơn vị theo hướng của các trục tọa độ Đêcac
i,j, k Cũng được dùng.
2-17.8 (11-13.5)
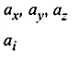
các thành phần Đêcac của vectơ a
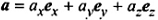
ax ex …..là các vectơ thành phần. Trong trường hợp các vectơ cơ sở là đã biết thì vectơ có thể viết là
a= (ax, ay, az).
...
...
...
r= xex + yey +zez là vectơ vị trí (vectơ bán kính) của điểm đó với các tọa độ X, y, z.
2-17.9 (11-7.19)
dijk
ký hiệu delta Kronecker
2-17.10
(11-7.20)
eijk
ký hiệu Levi-Civita
...
...
...
e132= e321= e213= -1
Mọi trường hợp khác eijk bằng 0.
2-17.11 (11-13.6)
a × b
tích vô hướng củaavà b
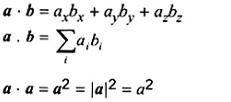
Trong các lĩnh vực đặc biệt, (a, b) cũng được dùng.
2-17.12 (11-13.7)
a x b
...
...
...
Trong hệ tọa độ Đêcac thuận, các thành phần là
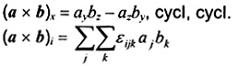
Xem 2-17.9.
2-17.13 (11-13.8)
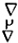
toán tử nabla
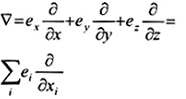
Toán tử này còn được gọi là “toán tử del”.
2-17.14 (11-13.9)
...
...
...
grad j
gradien của j
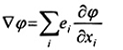
cần tránh viết toán tử grad trong mặt mỏng.
2-17.15 (11-13.10)
Ñ ×a
div a
div của a
...
...
...
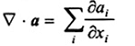
Ñ xa
rot a
rot của a
Các thành phần là
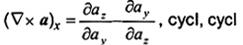
Phải tránh phép toán rot mặt cong và mỏng.
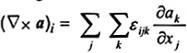
Xem 2-17.10.
2-17.17 (11-13.12)
...
...
...
D
toán tử Laplace
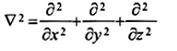
2-17.18 (11-13.13)
ÿ
toán tử Dalembert
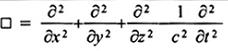
2-17.19
(11-13.14)
...
...
...
tenxơ T bậc hai
Để biểu thị tenxơ bậc hai, có thể dùng hai mũi trên trên chữ cái thay cho kiểu chữ không chân in đậm.
2-17.20
(11-13.15)
Txx, Txy, .., Tzz
T11, T12, … , T33
thành phần Đêcac của tenxơ T
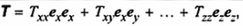
là các tenxơ thành phần.
...
...
...
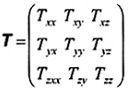
2-17.21 (11-13.16)
ab
aÄb
tích nhị nguyên,
tích tenxơ của hai vectơavà b
tenxơ bậc hai với các thành phần (ab)ij = aibj
2-17.22 (11-13.17)
TÄS
...
...
...
tenxơ bậc bốn với các thành phần
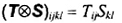
2-17.23 (11-13.18)
T×S
tích nội của hai tenxơ bậc hai T và S
tenxơ bậc hai với các thành phần
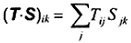
2-17.24
(11-13.19)
...
...
...
tích nội của tenxơ bậc hai T và vectơ a
vectơ với các thành phần
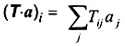
2-17.25 (11-13.20)
T:S
tích vô hướng của hai tenxơ bậc hai T và S
lượng vô hướng
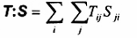
18 Phép biến đổi
...
...
...
Dấu, ký hiệu, biểu thức
Ý nghĩa, diễn đạt bằng lời
Chú thích và ví dụ
2-18.1
(-)
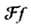
phép biến đổi Fourier của f
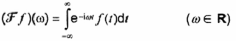
Thường ký hiệu bằng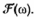 
...
...
...
cũng được dùng.
2-18.2
(-)
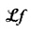
phép biến đổi Laplace của f
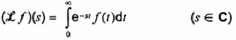
Thường ký hiệu bằng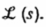 
Phép biến đổi Laplace hai vế cũng được sử dụng, tính theo công thức tương tự nhưng với âm vô cùng thay cho không.
2-18.3
...
...
...
3 (an)
phép biến đổi z của (an)
3 là phép toán tính theo dãy (an) chứ không phải là hàm số của an.
Phép biến đổi z hai vế cũng được sử dụng, tính theo công thức tương tự nhưng với âm vô cùng thay cho không.
2-18.4
(11-7.22)
H(x)
e(x)
...
...
...
U(x) cũng được dùng.
J (t) được dùng cho hàm bậc thang đơn vị của thời gian.
VÍ DỤ: (LH)(s)= 1/s (Re s > 0)
2-18.5
(11-7.21)
d(x)
phân bố delta Dirac, hàm delta Dirac
...
...
...
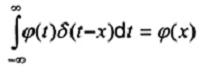
Tên đơn vị xung cũng được dùng.
VÍ DỤ: L d= 1
Xem thêm 2-18.6 và IEC 60027- 6:2006, mục 2.01.
2-18.6
(11-7.23)
f *g
tích chập của f và g
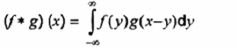
19 Các hàm đặc biệt
...
...
...
Số mục
Dấu, ký hiệu, biểu thức
Ý nghĩa, diễn đạt bằng lời
Chú thích và ví dụ
2-19.1
(-)
g
C
hằng số Euler
...
...
...
2-19.2
(11-14.19)
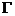(z)
hàm gamma
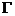(z) là hàm phân hình với các cực tại 0, -1.-2, -3,...
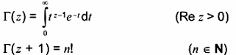
2-19.3 (11-14.23)
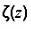
hàm zeta Riemann
...
...
...
2-19.4
(11-14.20)
B (z, w)
hàm beta
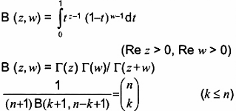
2-19.5 (11-14.21)
Ei x
tích phân hàm mũ
...
...
...
Đối với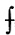 
, xem 2-11.20.
2-19.6
(-)
li x
tích phân loga
Đối với 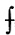, xem 2-11.20.
2-19.7
(-)
...
...
...
tích phân sin
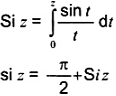được gọi là tích phân sin bù.
2-19.8
(-)
S(z)
C(z)
tích phân Fresnel
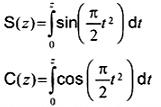
2-19.9 (11-14.22)
...
...
...
hàm sai số
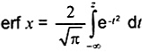
erfc x = 1- erf x được gọi là hàm sai số bù.
Trong thống kê học, hàm phân bố
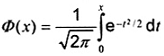được dùng
2-19.10
(11-14.16)
F (j, k)
tích phân eliptic không đầy đủ loại một
...
...
...
K(k)= F(p/2, k) là tích phân eliptic đầy đủ loại một (ở đây 0 < k < 1, k Î R).
2-19.11 (11-14.17)
E (j, k)
tích phân eliptic không đầy đủ loại hai
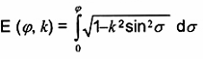
E(k)= E(p/2, k) là tích phân eliptic đầy đủ loại hai (ở đây 0 < k < 1, k Î R).
2-19.12 (11-14.18)
Õ(n, j , k)
tích phân eliptic không đầy đủ loại ba
...
...
...
Õ (n,k)= Õ (n, p/2, k) là tích phân eliptic đầy đủ loại ba (ở đây 0 < k < 1, k Î R).
2-19.13 (11-14.14)
F (a, b, c, z)
hàm siêu hình học
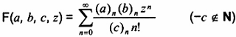
Đối với (a)n, (b)n và (c)n, xem 2-10.3. Nghiệm của
z(1 - z)y” + [c - (a +b+ 1 )z]y' - aby = 0
2-19.14
(11-14.15)
...
...
...
hàm siêu hình học suy biến
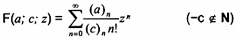
Đối với (a)n và (c)n, xem 2-10.3.
Nghiệm của zy” + [c - z]y’ -ay= 0
2-19.15
(11-14.8)
Pn(z)
đa thức Legendre
...
...
...
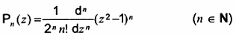
(1 -z2)y’’- 2zy’ + n(n+1 )y= 0
2-19.16 (11-14.9)
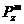(z)
hàm liên hợp Legendre
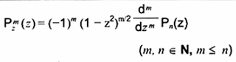
Nghiệm của
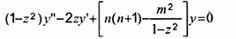
Hệ số (-1)m tuân theo lý thuyết chung của hàm cầu.
2-19.17
...
...
...
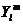(J,j)
hàm điều hòa cầu
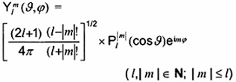
Nghiệm của
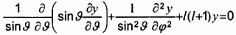
2-19.18
(11-14.11)
Hn(z)
đa thức Hermite
...
...
...
Nghiệm của
y”-2zy”+2ny=0 (n Î N)
2-19.19 (11-14.12)
Ln(z)
đa thức Laguerre
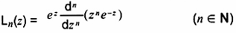
Nghiệm của zy”+ (1 - z )y’ + ny = 0
2-19.20 (11-14.13)
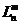(z)
...
...
...
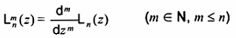
Nghiệm của
zy” + (m+1-z)y’ + (n-m)y = 0
2-19.21
(-)
Tn(z)
đa thức Chebyshev loại một
Tn(z) = cos (n arccos z) (n Î N)
Nghiệm của (1- z2)y”- z y’ + n2 y = 0
...
...
...
(-)
Un(z)
đa thức Chebyshev loại hai
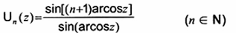
Nghiệm của
(1-z2)y” - 3 zy2 + n(n+2)y = 0
2-19.23
(11-14.1)
Jv(z)
...
...
...
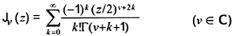
Nghiệm của
z2 y” + zy’ + (z2 - v2)y = 0
2-19.24
(11-14.2)
Nv (z)
hàm Neumann, hàm trụ loại hai
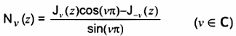
vế phải của công thức này được thay bằng giá trị giới hạn của nó nếu v Î Z. Yv (z) cũng được dùng.
...
...
...
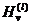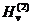(z)
(z)
hàm Hankel,
hàm trụ loại ba
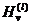(z) = Jv(z) + iNv(z)
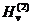(z) = Jv(z) + iNv(z)
(v Î C)
2-19.26
(11-14.4)
...
...
...
Kv (z)
hàm Bessel cải biên
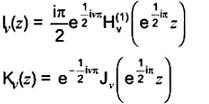
Nghiệm của
z2y” + zy’ - (z2 + v2)y = 0
2-19.27
(11-14.5)
jl(z)
hàm cầu Bessel
...
...
...
Nghiệm của
z2y” + 2zy’ + [z2 -l(l+1)]y = 0
2-19.28 (11-14.6)
nl(z)
hàm cầu Neumann
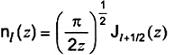
yl(z) cũng được dùng.
(l Î N)
2-19.29 (11-14.7)
...
...
...
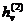(z)
hàm cầu Hankel
Hàm cầu Bessel cải biên (tương tự như 2-19.26) có thể được xác định và ký hiệu bằng il(z) và kl(z) tương ứng.
2-19.30
(-)
Ai(z)
Bi(z)
hàm Airy
...
...
...
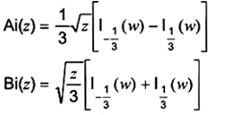
Nghiệm toàn phần của y” - zy = 0
Phụ lục A
(qui định)
Làm rõ các ký hiệu sử dụng
ISO/IEC 10646 cung cấp tên của các ký hiệu cùng với các loại mã được sử dụng khi các ký hiệu hoặc chữ cái này có mặt trong giao tiếp bằng máy. Mục đích chính của ISO/IEC 10646 là đưa ra dấu hiệu nhận biết rõ ràng cho chữ cái hoặc ký hiệu. Tiêu chuẩn này không mô tả đầy đủ các phương tiện và khái niệm của ISO/IEC 10646.
Unicode Consortium đã xuất bản quy định kỹ thuật liên quan [3] .Tuy nhiên, quy định Unicode Consortium [3] cũng bổ sung các thuộc tính của các ký tự (ví dụ như chúng là con số hay chữ in/chữ thường,...). Các thuộc tính này không quan trọng đối với tiêu chuẩn này.
Với mục đích của các bảng dưới đây, cả ISO/IEC 10646 và tài liệu tham khảo 3 đều đưa ra các quy định giống nhau, thường được gọi là “ký tự Unicode”.
ISO/IEC 10646 và Unicode được xây dựng như một dạng mở rộng của bảng chữ cái bao trùm “ASCII” (hệ Latinh cơ sở). Có một số cách mã hóa các ký hiệu và ký tự, trong đó phổ biến nhất là bộ mã 32-bit, bộ mã 16-bit - không phải toàn bộ các ký tự - và bộ mã có tên gọi UTF-8 có độ dài biến thiên, nhưng dẫn đến bộ mã ký tự ASCII trong một octave.
...
...
...
Phụ lục quy định này được đưa ra để làm rõ thêm về ký hiệu được sử dụng trong nội dung của tiêu chuẩn này, bất kể sử dụng phông chữ nào.
Bảng A.1 có bốn cột.
- Cột thứ nhất có hàng viện dẫn đến số mục trong nội dung tiêu chuẩn trong đó ký hiệu được sử dụng. (Tiêu đề: “Số mục”).
- Cột thứ hai lặp lại ký hiệu với cùng phông chữ, vị trí, định dạng và cỡ được dùng trong nội dung tiêu chuẩn này. (Tiêu đề: “Dấu, ký hiệu”).
- Cột thứ ba nêu tên gọi trong ISO/IEC 10646 và Unicode [3] (chúng giống hệt nhau). Ví dụ: “TÍCH CƠ SỐ N” (ngược với “CHỮ HY LẠP HOA Pl”) hoặc “TỔNG CƠ SỐ N” (ngược với “CHỮ HY LẠP HOA SIGMA”). [Tiêu đề: “Tên của ký hiệu (xem ISO/IEC 10646)”.] Thực tế là một số tên gọi trong ISO/IEC 10646 không nhất quán với thực tiễn và sử dụng hiện hành của ký hiệu đi kèm và, đặc biệt là, khác với cách sử dụng trong tiêu chuẩn này.
- Cột thứ tư đưa ra (để dễ tham chiếu và làm rõ) bộ mã 16 bit ấn định cho ký hiệu ở cả ISO/IEC 10646 và Unicode [3]. UTF-8 (mã hóa có độ dài biến thiên, chỉ dùng một octave đối với các ký tự trong bộ ký tự ASCII) và bộ mã 32 bit - và các bộ khác - cũng có thể sử dụng. Tiêu đề: “Giá trị cơ số 16 của ký hiệu (xem ISO/IEC 10646”.]
CHÚ THÍCH: Trong các phần khác của bộ TCVN 7870 (ISO 80000), “kiểu chữ” (tháng hoặc nghiêng, không đậm hoặc đậm, hoặc đậm nghiêng) cũng có cùng ý nghĩa và phải được gắn thêm vào. Tuy nhiên, trong tiêu chuẩn này, tất cả các ký hiệu đều ở kiểu chữ thẳng và không có cột nào trong bảng dưới đây nêu thông tin như vậy.
Thông tin bổ sung về các ký hiệu dùng trong toán học được cho trong tài liệu tham khảo [4]
Bảng A.1
...
...
...
Dấu, ký hiệu
Tên ký hiệu (xem ISO/IEC 10646)
Giá trị cơ số 16 của ký hiệu (Xem ISO/IEC 10646)
2-4.1
∧
VÀ
2227
2-4.2
∨
...
...
...
2228
2-4.3
¬
DẤU PHỦ ĐỊNH
00AC
2-4.4
⇒
MŨI TÊN KÉP SANG PHẢI
21D2
...
...
...
⇔
MŨI TÊN KÉP TRÁI PHẢI
21D4
2-4.6
∀
VỚI MỌI
2200
2-4.7
∃
...
...
...
2203
2-5.1
∈
PHẦN TỬ CỦA
2208
2-5.2
∉
KHÔNG PHẢI PHẦN TỬ CỦA
2209
...
...
...
|
ĐƯỜNG THẲNG ĐỨNG
007C
2-5.5
|
ĐƯỜNG THẲNG ĐỨNG
007C
2-5.6
∅
...
...
...
2205
2-5.7
⊆
TẬP CON CỦA HOẶC BẰNG
2286
2-5.8
⊂
TẬP CON CỦA
2282
...
...
...
∪
HỢP
222A
2-5.10
∩
GIAO
2229
2-5.11
⋃
...
...
...
22C3
2-5.12
⋂
GIAO CƠ SỐ N
22C2
2-5.13
∖
DẤU TRỪ TẬP HỢP
2216
...
...
...
∁
BÙ
2201
2-5.16
×
DẤU NHÂN
00D7
2-5.17
Õ
...
...
...
220F
2-6.1
ℕ
N HOA KÉP
2115
2-6.2
ℤ
Z HOA KÉP
2124
...
...
...
ℚ
Q HOA KÉP
211A
2-6.4
ℝ
R HOA KÉP
211D
2-6.5
ℂ
...
...
...
2102
2-6.6
ℙ
P HOA KÉP
2119
2-7.1
=
DẤU BẰNG
003D
...
...
...
¹
KHÁC
2260
2-7.3
≔
HAI CHẤM BẰNG
2254
2-7.3
≝
...
...
...
225D
2-7.4
≙
ƯỚC LƯỢNG BẰNG
2259
2-7.5
≈
XẤP XỈ BẰNG
2248
...
...
...
≃
TIỆM CẬN BẰNG
2243
2-7.7
~
TƯƠNG ĐƯƠNG
223C
2-7.7
∝
...
...
...
221D
2-7.8
ĐỒNG DẠNG VỚI
2245
2-7.9
<
DẤU NHỎ HƠN
003C
...
...
...
>
DẤU LỚN HƠN
003E
2-7.11
£
NHỎ HƠN HOẶC BẰNG
2264
2-7.12
³
...
...
...
2265
2-7.13
≪
RẤT NHỎ HƠN
226A
2-7.14
≫
RẤT LỚN HƠN
226B
...
...
...
¥
VÔ CÙNG
221E
2-7.16
→
MŨI TÊN SANG PHẢI
2192
2-7.17
∣
...
...
...
2223
2-7.18
º
ĐỒNG NHẤT BẰNG
2261
2-7.19
<
DẤU NGOẶC NHỌN TRÁI
27E8
...
...
...
>
DẤU NGOẶC NHỌN PHẢI
27E9
2-8.1
∥
SONG SONG VỚI
2225
2-8.2
^
...
...
...
27C2
2-8.3
Ð
GÓC
2220
2-9.1
+
DẤU CỘNG
002B
...
...
...
-
DẤU TRỪ
2212
2-9.3
±
DẤU CỘNG TRỪ
00B1
2-9.4
∓
...
...
...
2213
2-9.5
⋅
TOÁN TỬ CHẤM
22C5
2-9.5
×
DẤU NHÂN
00D7
...
...
...
/
DẤU GẠCH CHÉO
002F
2-9.7
å
TỔNG CƠ SỐ N
2211
2-9.8
Õ
...
...
...
220F
2-9.10
Ö
CĂN BẠC HAI
221A
2-9.12
<
DẤU NGOẶC NHỌN TRÁI
27E8
...
...
...
>
DẤU NGOẶC NHỌN PHẢI
27E9
2-9.16
|
ĐƯỜNG THẲNG ĐỨNG
007C
2-9.17
ë
...
...
...
230A
2-9.17
û
SÀN PHẢI
230B
2-9.18
é
TRẦN TRÁI
2308
...
...
...
ù
TRẦN PHẢI
2309
2-11.3
®
MŨI TÊN SANG PHẢI
2192
2-11.4
...
...
...
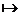
21A6
2-11.7
∘
PHÉP VÒNG
2218
2-11.11
∆
SỐ GIA
2206
...
...
...
′
PHẨY TRÊN
2032
2-11.15
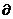
VI PHÂN TỪNG PHẦN
2202
2-11.16
d
...
...
...
0064
2-11.17
d
CHỮ DELTA THƯỜNG HY LẠP
03B4
2-11.18
ò
TÍCH PHÂN
2228
...
...
...
òò
TÍCH PHÂN KÉP
222C
2-11.19
∮
TÍCH PHÂN ĐƯỜNG CONG KÍN
222E
2-11.19
∯
...
...
...
222F
2-11.20
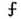
TÍCH PHÂN PHẦN HỮU HẠN
2A0D
2-17.11
⋅
TOÁN TỬ CHẤM
22C5
...
...
...
×
DẤU NHÂN
00D7
2-17.13
∇
NABLA
2207
2-17.17
∆
...
...
...
2206
2-17.18
DẤU VUÔNG TRẮNG
25A1
2-17.21
⊗
NHÂN TRÒN
2297
...
...
...
ℱ
CHỮ F HOA
2131
2-18.2
ℒ
CHỮ L HOA
2112
2-18.3
...
...
...
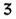
2128
2-18.6
∗
TOÁN TỬ SAO
2217
THƯ MỤC TÀI LIỆU THAM KHẢO
[1] ISO/IEC 10646:2003, Information technology- Universal Multiple-Octet Coded Character Set(UCS) (Công nghệ thông tin - Bộ mã ký tự 8 bit chung)
[2] IEC 60027-6:2006, Letter symbols to be used in electrical technology - Part 6: Control technology (Ký hiệu bằng chữ dùng trong kỹ thuật điện - Phần 6: Kỹ thuật điều khiển)
...
...
...
[4] Unicode Technical Report #25 - Unicode support for mathematics. The UnicodeConsortium. (Reading, MA, Addison-Wesley) URL: http://www.unicode.org/reports/tr25
MỤC LỤC
Lời nói đầu
Lời giới thiệu
1. Phạm vi áp dụng
2. Tài liệu viện dẫn
3. Biến số, hàm số và toán tử
4. Logic toán
...
...
...
6. Tập và khoảng số tiêu chuẩn
7. Dấu và ký hiệu hỗn hợp
8. Hình học sơ cấp
9. Các phép toán
10. Tổ hợp
11. Hàm số
12. Hàm mũ và hàm loga
13. Hàm số vòng và hàm hypecbol
14. Số phức
...
...
...
16. Hệ tọa độ
17. Đại lượng vô hướng, vectơ và tenxơ
18. Phép biến đổi
19. Các hàm đặc biệt
Phụ lục A (qui định) Làm rõ các ký hiệu sử dụng
Thư mục tài liệu tham khảo