Khái niệm về tam giác vuông cân

Tam giác vuông cân là một tam giác mà có một góc vuông (90 độ) và hai cạnh còn lại có độ dài bằng nhau. Điều này làm cho tam giác này có sự kết hợp đặc biệt của cả hai yếu tố: tính đối xứng và sự rõ ràng của góc vuông. Nếu bạn đã học về các tam giác cơ bản, thì tam giác vuông cân là một ví dụ đặc biệt dễ nhận ra trong hình học.
Đặc điểm của tam giác vuông cân:
Với tam giác vuông cân, có một số điểm lưu ý mà bạn cần nhớ:
- Hai cạnh bằng nhau: Đó là hai cạnh góc vuông, gọi là "cạnh kề" trong tam giác. Bởi vì chúng bằng nhau, tam giác vuông cân trở nên đối xứng.
- Góc còn lại: Ngoài góc 90 độ, hai góc còn lại của tam giác đều bằng nhau và mỗi góc là 45 độ. Vậy là bạn có một góc vuông và hai góc cân.
- Tính đối xứng: Nếu bạn gấp đôi tam giác này theo đường phân giác đi qua góc vuông, bạn sẽ thấy hai phần của tam giác hoàn toàn trùng khớp với nhau. Tính đối xứng này làm cho tam giác vuông cân trở nên đặc biệt dễ phân tích và sử dụng trong các bài toán hình học.
Công thức tính cạnh huyền tam giác vuông cân
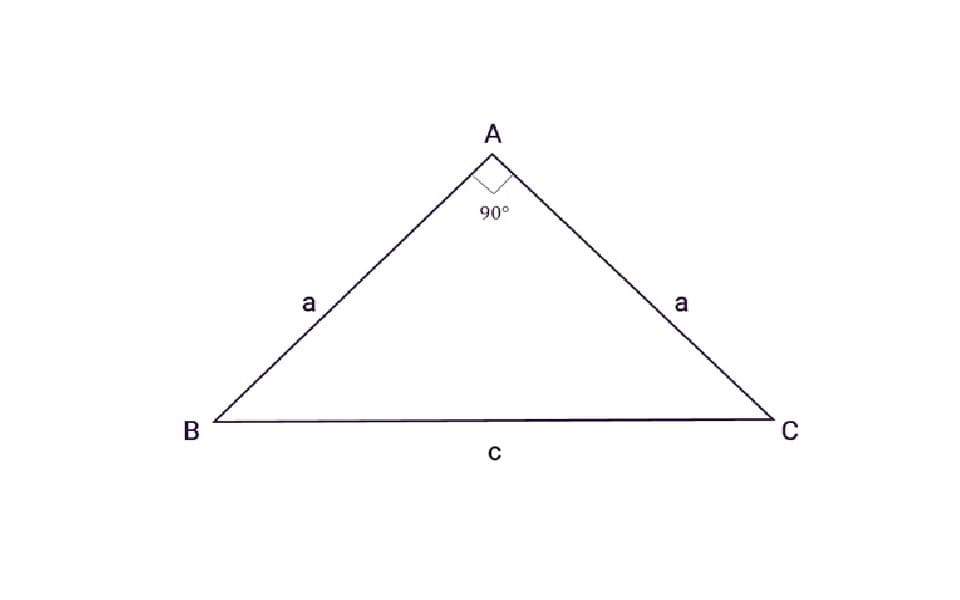
Công thức tính cạnh huyền tam giác vuông cân không chỉ dễ nhớ mà còn giúp bạn giải quyết nhiều bài toán phức tạp một cách đơn giản. Dưới đây là dạng công thức tổng quát để tính cạnh huyền trong tam giác đặc biệt này:
Công thức tổng quát:
Trong tam giác vuông cân, hai cạnh góc vuông có độ dài bằng nhau và chúng ta gọi độ dài đó là a. Vậy cạnh huyền c (tức là cạnh dài nhất, đối diện với góc vuông) sẽ được tính theo công thức là:
c=a2c = a \sqrt{2}
Công thức này cho phép bạn tính được độ dài của cạnh huyền chỉ bằng việc biết độ dài của một trong hai cạnh vuông.
Chứng minh công thức:
Ta sẽ sử dụng Định lý Pytago, định lý này nói rằng trong một tam giác vuông, tổng bình phương của hai cạnh góc vuông sẽ bằng bình phương của cạnh huyền.
Áp dụng định lý vào tam giác vuông cân của chúng ta, với hai cạnh góc vuông bằng a, ta có:
c2=a2+a2c^2 = a^2 + a^2
Điều này có nghĩa là:
c2=2a2c^2 = 2a^2
Bây giờ, ta lấy căn bậc hai của cả hai vế để tìm cc:
c=2a2=a2c = \sqrt{2a^2} = a\sqrt{2}
Chúng ta đã chứng minh được rằng cạnh huyền bằng a2a\sqrt{2}.
Ví dụ minh họa:
Cho một tam giác vuông cân với mỗi cạnh góc vuông dài 5 cm. Vậy cạnh huyền sẽ là bao nhiêu?
Dựa vào công thức c=a2c = a\sqrt{2}, ta thay a=5a = 5 vào:
c=5×2≈5×1.414=7.07 cmc = 5 \times \sqrt{2} \approx 5 \times 1.414 = 7.07 \, \text{cm}
Vậy cạnh huyền của tam giác vuông cân này dài xấp xỉ 7,07 cm.
Bài tập vận dụng và lời giải
Khi học về tam giác vuông cân, nên áp dụng ngay kiến thức để hiểu sâu hơn và làm quen với các dạng bài tập. Dưới đây là một số bài tập cơ bản và nâng cao, kèm theo lời giải chi tiết.
Bài tập cơ bản:
Bài 1:Cho một tam giác vuông cân có độ dài mỗi cạnh góc vuông là 6 cm. Tính độ dài cạnh huyền.
Bài 2:Một tam giác vuông cân có diện tích là 32 cm². Tính độ dài cạnh huyền của tam giác.
Bài tập nâng cao:
Bài 3:Cho một tam giác vuông cân có cạnh huyền dài 10 cm. Tính chu vi và diện tích của tam giác này.
Bài 4:Tam giác ABC là tam giác vuông cân với góc A = 90°, biết độ dài cạnh AB = 7 cm. Tính chu vi và diện tích của tam giác ABC, đồng thời tính chiều cao hạ từ A xuống cạnh BC.
Giải đáp bài tập:
Giải bài 1:Dùng công thức tính cạnh huyền trong tam giác vuông cân, chúng ta có:
c=a2c = a\sqrt{2}
Với a=6a = 6, ta thay vào công thức:
c=62≈6×1.414=8.49 cmc = 6\sqrt{2} \approx 6 \times 1.414 = 8.49 \, \text{cm}
Vậy cạnh huyền của tam giác dài xấp xỉ 8.49 cm.
Giải bài 2:Diện tích của tam giác vuông cân được tính bằng công thức:
S=12a2S = \frac{1}{2} a^2
Với S=32 cm2S = 32 \, \text{cm}^2, ta có:
32=12a2 ⇒ a2=64 ⇒ a=8 cm32 = \frac{1}{2} a^2 \quad \Rightarrow \quad a^2 = 64 \quad \Rightarrow \quad a = 8 \, \text{cm}
Áp dụng công thức tính cạnh huyền:
c=82≈8×1.414=11.31 cmc = 8\sqrt{2} \approx 8 \times 1.414 = 11.31 \, \text{cm}
Vậy cạnh huyền dài khoảng 11.31 cm.
Giải bài 3:Biết cạnh huyền c=10c = 10, ta sử dụng công thức ngược lại để tìm độ dài cạnh góc vuông:
a=c2=102≈101.414=7.07 cma = \frac{c}{\sqrt{2}} = \frac{10}{\sqrt{2}} \approx \frac{10}{1.414} = 7.07 \, \text{cm}
Chu vi tam giác:
P=a+a+c=7.07+7.07+10=24.14 cmP = a + a + c = 7.07 + 7.07 + 10 = 24.14 \, \text{cm}
Diện tích tam giác:
S=12a2=12×7.072≈25 cm2S = \frac{1}{2} a^2 = \frac{1}{2} \times 7.07^2 \approx 25 \, \text{cm}^2
Giải bài 4:Với tam giác vuông cân ABC, ta có AB = AC = 7 cm.
Chu vi tam giác:
P=AB+AC+BC=7+7+72≈7+7+9.9=23.9 cmP = AB + AC + BC = 7 + 7 + 7\sqrt{2} \approx 7 + 7 + 9.9 = 23.9 \, \text{cm}
Diện tích tam giác:
S=12×AB×AC=12×7×7=24.5 cm2S = \frac{1}{2} \times AB \times AC = \frac{1}{2} \times 7 \times 7 = 24.5 \, \text{cm}^2
Chiều cao hạ từ A xuống BC:
Chiều cao này chính là cạnh góc vuông trong tam giác nhỏ vuông cân hạ từ A, ta có:
h=BC2=722≈4.95 cmh = \frac{BC}{2} = \frac{7\sqrt{2}}{2} \approx 4.95 \, \text{cm}
Ứng dụng thực tế

Công thức tính cạnh huyền trong tam giác vuông cân có rất nhiều ứng dụng trong đời sống hàng ngày, đặc biệt là trong các lĩnh vực như kiến trúc, xây dựng, thiết kế đồ họa và cả vật lý.
Kiến trúc và xây dựng:
Một trong những yếu tố quan trọng nhất khi thiết kế là tính đối xứng và sự ổn định của các công trình. Tam giác vuông cân trở thành một trong những phương pháp tốt nhất trong việc đảm bảo rằng các cấu trúc chịu lực một cách cân bằng.
Ví dụ, khi xây dựng mái nhà, đặc biệt là mái nhà dạng tam giác, công thức tính cạnh huyền giúp các kỹ sư xác định được chiều dài của thanh chống chính xác dựa trên chiều cao và chiều dài của phần mái. Điều này không chỉ giúp đảm bảo tính thẩm mỹ mà còn đảm bảo sự an toàn và ổn định của công trình.
Thiết kế đồ họa và kỹ thuật:
Trong thế giới của thiết kế, từ việc cắt hình, vẽ các đường thẳng chính xác, đến việc tạo ra các hình ảnh đối xứng, tam giác vuông cân đóng vai trò rất quan trọng. Chẳng hạn, khi tạo ra các biểu tượng hoặc hình minh họa có tính đối xứng, công thức tính cạnh huyền giúp bạn xác định kích thước và tỷ lệ của các thành phần một cách chính xác mà không cần phải thử nghiệm nhiều lần. Điều này cũng áp dụng cho việc dựng mô hình 3D, nơi các bề mặt phẳng thường phải được xác định độ dài chính xác để đảm bảo rằng các mô hình không bị méo mó.
Vật lý và kỹ thuật:
Trong lĩnh vực kỹ thuật, khi bạn làm việc với các loại lực tác động, đặc biệt là lực phân bố theo các hướng khác nhau, tam giác vuông cân giúp bạn dễ dàng phân tích và tính toán thành phần của lực. Ví dụ, khi một vật đang chịu tác động của hai lực cùng độ lớn nhưng khác hướng, ta có thể sử dụng tam giác vuông cân để tính toán độ lớn của lực tổng hợp. Điều này giúp kỹ sư đưa ra các phương án thiết kế tối ưu, giảm thiểu rủi ro trong quá trình xây dựng và vận hành.
Xem thêm:
Khám phá các cách tính cạnh huyền tam giác vuông
Kết Luận
Như vậy, tính cạnh huyền tam giác vuông cân hỗ trợ chúng ta nhiều ứng dụng thực tế trong cuộc sống. Sự đối xứng, góc vuông và mối liên hệ giữa các cạnh của tam giác vuông cân giúp chúng ta hiểu rõ hơn về các định lý phức tạp liên quan trong hình học hay cả trong ứng dụng thực tế. Gia sư Học là Giỏi hi vọng bạn sẽ nắm vững và áp dụng cách tính cạnh huyền này trong đời sống hiện tại nhé.