Trong chương trình toán lớp 10 đại số, tập hợp là bài toán đơn giản nhưng là nền tảng mà bất cứ học sinh nào cũng phải nắm rõ để vận dụng cho những nội dung tiếp theo.
Mục lục
I. Tập hợp 1, Khái niệm tập hợp 2, Tập con và tập hợp bằng nhau II. Các phép toán tập hợp 1, Giao của hai tập hợp 2, Hợp của hai tập hợp 3, Hiệu và phần bù của hai tập hợp III. Các tập hợp số
Để hiểu một các chi tiết nhất về tập hợp, thầy Lưu Huy Thưởng (giáo viên môn Toán tại Hệ thống Giáo dục HOCMAI) đã chỉ rõ cho các em học sinh về thế nào là tập hợp, các phép toán tập hợp và các tập hợp số giúp học sinh làm bài tập một cách hiệu quả.
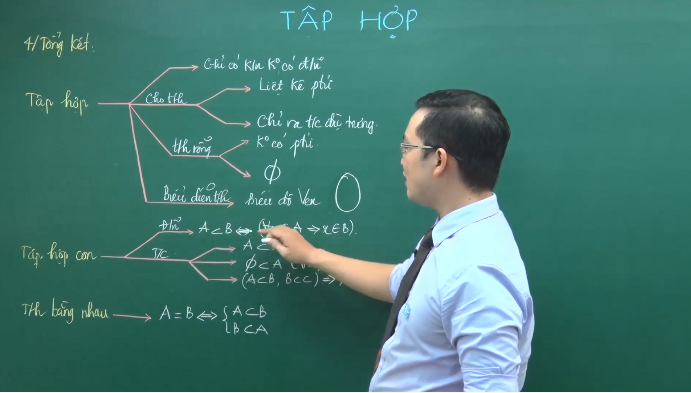
1, Khái niệm tập hợp
a, Khái niệm tập hợp
- Khái niệm tập hợp bao gồm phần tử có chung một hoặc một vài tính chất nào đó.Ví dụ: “Tập hợp các số tự nhiên chia hết cho 3 và nhỏ hơn 20” : Là tập hợp các số tự nhiên thỏa mãn 2 tính chất vừa chia hết cho 3 và nhỏ hơn 20.Kí hiệu: Tập hợp được kí hiệu bằng chữ cái in hoa.Các phần tử được ghi trong hai dấu ngoặc nhọn { }, cách nhau bởi dấu , hay ;Ví dụ: a là phần tử thuộc tập hợp X kí hiệu là a ∈ X b, Cách cho một tập hợp Một tập hợp có thể được xác định bằng cách chỉ ra tính chất đặc trưng cho các phần tử của nó. Vậy ta có thể xác định một tập hợp bằng 2 cách sau:
- Liệt kê các phần tử : C = {phần tử}
Ví dụ: C = {4, 2, 1, 3}
- Chỉ ra tính chất đặc trưng của các phần tử
Chỉ rõ tính chất đặc trưng của các phần tử giúp thâu tóm ngắn gọn những tập hợp dài
Ví dụ: Tập hợp các số tự nhiên nhỏ hơn 4
c, Tập rỗng
Khái niệm: Tập rỗng là tập hợp không có phần tử nào
Kí hiệu:
Ví dụ:
2, Tập con và tập hợp bằng nhau
a, Tập con
Cho 2 phần tử A và B, mọi phần tử thuộc A đều thuộc B khi đó A là tập con của B.
Kí hiệu: A⊂B
Tính chất:
- Nếu A là con của B, B là con của C thì A là con của C
- Mọi tập hợp đều là tập con của chính nó, nghĩa là tập A là con của tập A, tập B là con của tập B
- Tập rỗng là tập con của mọi tập hợp
b, Tập hợp bằng nhau: A là con của tập A, B là con của tập B thì ta nói rằng ta nói rằng tập hợp A bằng tập hợp B hay ta nói rằng mọi phần tử thuộc tập hợp A đều thuộc tập hợp B và ngược lại.
Kí hiệu: A=B⇔ (A⊂B) và (B⊂A)
1, Giao của hai tập hợp
Khái niệm: Tập hợp C gồm các phần tử vừa thuộc A, vừa thuộc B được gọi là giao của A và B.
Ký hiệu
Ví dụ
2, Hợp của hai tập hợp
Khái niệm: Tập hợp C gồm các phần tử vừa thuộc A hoặc vừa thuộc B được gọi là hợp của A và B.
Ký hiệu
Ví dụ
3, Hiệu và phần bù của hai tập hợp
a, Hiệu của hai tập hợp
Khái niệm: Tập hợp C gồm các phần tử vừa thuộc A nhưng không thuộc B được gọi là hiệu của A và B.
Ký hiệu
Ví dụ
b, Phần bù của hai tập hợp
Khái niệm: Khi B là con của A thì A\B gọi là phần bù của B trong A.
Ký hiệu
Ví dụ
Tập hợp các số tự nhiên N,N*
Tập hợp các số nguyên Z
Tập hợp các số hữu tỷ Q
Tập hợp các số thực ℝ
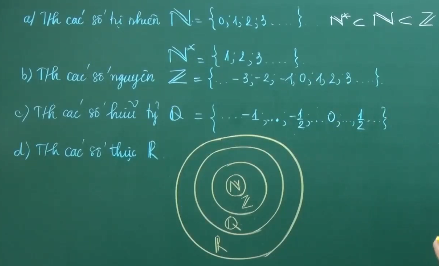
Một số tập con của tập số thực ℝ










![SH Mode 125 [2023] | Nam Sương Motor](/uploads/blog/2024/12/25/c8acfe940318b35b0b101662fdc1ad496829fb83-1735141705.jpg)









